Space–Time Tradeoffs - Models of Computation: Exploring the Power of Computing - page 463

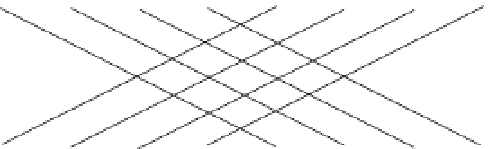
Figure 10.1 An FFT graph F ( 3 ) on n = 2 3 inputs. Input vertices are on the bottom; edges are
directed upward. Four pebbles are shown on the graph when pebbling the leftmost output.

input variables are held in an auxiliary random-access machine so that it can access them in
arbitrary order, a condition not imposed on pebble games. It follows that inputs to a pebble
game can be fetched in advance, since the times at which they are needed are data-independent.
Second, lower bounds on the exchange of space for time with branching programs are harder to
obtain due to their increased flexibility. Third, straight-line programs are used in many prob-
lems, such as integer multiplication, convolution, matrix multiplication, and discrete Fourier
transform, and the pebble game gives the relevant lower bounds. For other problems, such as
sorting and merging, the branching programmodel is the model of choice since these problems
are typically solved with branching programs. We expand upon this topic in Section 10.9.1 .

10.1.2 Playing the Pebble Game
The pebble game is illustrated in Fig. 10.1 by pebbling the FFT graph F ( 3 ) with eight inputs
and 24 non-input vertices. This graph has the property that the set of paths from input vertices
to an output vertex forms a complete balanced binary tree. (See Fig. 10.2 .) It follows that we
can pebble the FFT graph by pebbling each of the trees. Since two of the eight outputs share
the same tree at the next lower level, we can pebble two outputs at the same time.
Binary trees form an important class of graphs. A complete balanced binary tree of depth
4 is illustrated in Fig. 10.2 . (The depth of a directed tree is the number of edges on the longest
path from an input vertex to the output (or root) vertex.) This tree has 16 input vertices and
one output vertex. A complete balanced binary tree of depth 0, T ( 0 ) , consists of a single
vertex. A complete balanced binary tree of depth d> 0, T ( d ) , consists of a root vertex and
two copies of T ( d

1 ) whose root vertices each have one edge directed from them to the
root vertex of the full tree. Thus in Fig. 10.2 the complete balanced binary tree of depth four
T ( 4 ) is constructed of two copies of T ( 3 ) , which in turn are each constructed of two copies of
T ( 2 ) , and so on. It follows by straightforward induction that a complete balanced binary tree
of depth d has 2 d

−

inputs and 2 d + 1

− 1 vertices. (See Problem 10.8 .)