Information Technology Reference
In-Depth Information
DEFINITION
9.6.4
Let
f
(
n
,
m
,
p
)
=(
f
1
,
f
2
,
...
,
f
p
)
,whereeach
f
r
:
B
n
+
m
→B
≤
r
≤
p
,
,
1
is a monotone function on
n
-tuple
x
and
m
-tuple
y
;thatis,
f
r
(
x
,
y
)
∈B
.
f
(
n
,
m
,
p
)
is a
bilinear
form
if each prime implicant of each
f
r
,
1
≤
r
≤
p
,containsonevariableof
x
and one of
y
.
Afunction
f
(
n
,
m
,
p
)
is a
semi-disjoint bilinear form
if in addition
PI
(
f
r
)
∩
PI
(
f
s
)=
∅
for
r
=
s
and each variable is contained in at most one prime implicant of any one function.
Before deriving a lower bound on the number of gates needed for a semi-disjoint bilinear
form, we introduce a new replacement rule peculiar to these forms.
LEMMA
9.6.2
No gate of a monotone circuit of minimal size for a semi-disjoint bilinear form
f
(
n
,
m
,
p
)
computes a function
g
whose prime implicants include either two variables of
x
or of
y
.
Proof
We suppose that a minimal monotone circuit does contain a gate
g
whose prime
implicants contain either two variables of
x
or two of
y
and show that a contradiction
results. Without loss of generality, assume that
PI
(
g
)
contains
x
i
and
x
j
,
i
=
j
.Ifthereis
agate
g
satisfying this hypothesis, there is one that is closest to an input variable. This must
be an
OR
gate because
AND
gates increase the length of prime implicants. Because the gate
in question is closest to inputs, at least one of
x
i
and
x
j
is either an input to this
OR
gate or
is the input to some
OR
gate that is on a path of
OR
gatestothisgate.(SeeFig.
9.12
.)
A simple proof by induction on its circuit size demonstrates that if a circuit for
f
(
n
,
m
,
p
)
=(
f
1
,
...
,
f
p
)
contains a gate computing
g
then
f
r
,1
≤
r
≤
p
, can be written as follows
(see Problem
9.36
):
f
r
(
x
,
y
)=(
p
r
(
x
,
y
)
∧
g
(
x
,
y
))
∨
q
r
(
x
,
y
)
(9.1)
Here
p
r
(
x
,
y
)
and
q
r
(
x
,
y
)
are Boolean functions. Of course, if for no
r
is
f
r
afunctionof
g
,thenwecanset
p
r
(
x
,
y
)=
0 and the circuit is not minimal.
If
f
r
depends on
g
,
p
r
(
x
,
y
)
=
1 because otherwise both
x
i
and
x
j
are prime implicants of
f
r
, contradicting its definition. Also,
PI
(
p
r
(
x
,
y
))
cannot have any monoms containing one or more instances of a variable in
x
or two or
more instances of variables in
y
because when
AND
ed with
g
they produce monoms that
could be removed by Rule (a) of Definition
9.6.2
and the circuit would not be minimal. It
follows that
PI
(
p
r
(
x
,
y
))
can contain only single variables of
y
. But this implies that for
some
k
,
y
k
∧
=
0. However,
p
r
(
x
,
y
)
g
∈
I
(
f
r
)
, which together with the fact that
x
i
,
x
j
∈
PI
(
g
)
implies that
g
x
1
x
2
x
3
x
4
Figure 9.12
If
PI
(
g
)
for a gate
g
contains
x
i
and
x
j
, then either
x
i
or
x
j
is input to an
OR
gate on a path of
OR
gates to
g
.
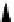




























Search WWH ::

Custom Search