Circuit Complexity - Models of Computation: Exploring the Power of Computing - page 409

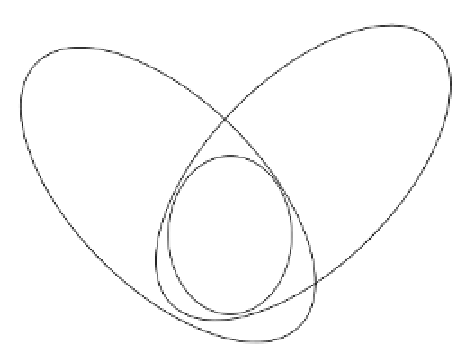
A 2

h − 1 ( 1 ) g − 1 ( 1 )

f − 1 ( 1 )

￿￿￿￿ ￿￿￿￿

￿￿￿￿ ￿￿￿￿

A

￿￿￿￿ ￿￿￿￿

B

Figure 9.7 The relationships among the sets f − 1 ( 1 ) , g − 1 ( 1 ) , h − 1 ( 1 ) , A 2 ,and h − 1

( 0 ) .

By the identity n 1 /a 1 + n 2 /a 2 ( n 1 + n 2 ) 2 / ( a 1 + a 2 ) , which holds for positive integers

(see Problem 9.3 ), the desired result follows because

≥

| A | | A 1 | | A 2 |

= + .

Krapchenko's method is easily applied to the parity function f ( n )
⊕

. We need only let A

= 2 n− 1 .) Then

( B )contain n -tuples having an even (odd) number of 1's.

| A | = | B |

(

= n 2 n− 1 because for any vector in A there are exactly n vectors in B that are |N ( A , B ) |

neighbors of it. It follows that L Ω 0 f ( n )

≥ n 2 .

⊕

9.5 The Power of Negation
As a prelude to the discussion of monotone circuits for monotone functions in the next sec-
tion, we consider the minimum number of negations necessary to realize an arbitrary Boolean
function f :

m . From Problem 2.12 on dual-rail logic we know that every such
function can be r eal iz ed by a monotone circuit in which both the variables x 1 , x 2 , ... , x n and
their negations x 1 , x 2 , ... , x n are provided as inputs. Furthermore, every such circuit need
have only at most twice as many AND and OR gates as a minimal circuit over Ω 0 , the standard
basis. Also, the depth of the dual-rail logic circuit of a function is at m o st one m o re than the
depth of a minimal-depth circuit, the extra depth being that to form x 1 , x 2 , ... , x n .
Let f ( n )
NEG

n

B →B

n be defined by f ( n ) n

NEG ( x 1 , x 2 , ... , x n )=( x 1 , x 2 , ... , x n ) .As
shown in Lemma 9.5.1 , this function can be realized by a circuit of size O ( n 2 log n ) and
depth O (log 2 n ) over Ω 0 using

: B →B

negations. This implies that most Boolean
functions on n variables can be realized by a circuit whose size and depth are within a factor of
about 2 of their minimal values when the number of negations is

log 2 ( n + 1 )

log 2 ( n + 1 ) .

THEOREM 9.5.1 Every Boolean function on n variables, f : B

n m , can be realized by a

→B

circuit containing at most negations. Furthermore, the minimal size and depth of

such circuits is at most 2 C Ω 0 ( f )+ O ( n 2 log n ) and D Ω 0 ( f )+ O (log 2 n ) , respectively, where
C Ω 0 ( f ) and D Ω 0 ( f ) are the circuit size and depth of f over the standard basis Ω 0 .

log 2 ( n + 1 )