Information Technology Reference
In-Depth Information
f
(
l
)
mux
x
|
a
|
,
l−
1
x
|
a
|
,0
x
|
a
|
,
l−
2
y
L−
1
y
0
...
a
k−
1
a
k−
1
a
k−
1
f
(
k
)
f
(
k
)
f
(
k
)
mux
mux
mux
a
1
a
1
a
1
a
0
a
0
a
0
x
K−
1,
l−
1
x
0,
l−
1
x
K−
1,
l−
2
x
0,
l−
1
x
K−
1,0
x
0,0
Figure 9.5
The schema used to construct a circuit of fan-out 1 for the indirect storage access
function
f
(
k
,
l
)
ISA
.
n/l
we see that
f
(
k
,
l
)
ISA
K
=
2
k
has 2
l
+
l
2
k
+
k
=
O
(
n
)
variables and that its formula size is
≥
1
)
L
Ω
f
(
k
)
mux
+
L
Ω
f
(
l
)
mux
,whichis
O
(
n
2
/
log
2
n
)
, as summarized in Lemma
9.4.1
.
2
(
2
l
−
LEMMA
9.4.1
Let
2
l
=
n
and
k
=
log
2
n/l
. Then the formula size of
f
(
k
,
l
)
k
+
lK
+
L
:
B
→
ISA
B
satisfies the following bound:
L
Ω
f
(
k
,
l
)
ISA
=
O
(
n
2
/
log
2
n
)
We now introduce Neciporuk's method, by which it can be shown that this bound for
f
(
k
,
l
)
ISA
is optimal to within a constant multiplicative factor.
9.4.1 The Neciporuk Lower Bound
The Neciporuk lower-bound method uses a partition of the variables
X
=(
x
1
,
x
2
,
...
,
x
n
)
of
a Boolean function
f
(
n
)
:
into disjoint sets
X
1
,
X
2
,
...
,
X
p
.Thatis,
X
=
i
=
1
X
i
n
B
→B
and
X
i
∩
X
j
=
∅
for
i
=
j
. The lower bound on the formula size of
f
is stated in terms of
r
X
j
(
f
)
,0
p
,the
number of subfunctions of
f
when restricted to variables in
X
j
.
That is,
r
X
j
(
f
)
is the number of different subfunctions of
f
in the variables in
X
j
obtained
by ranging over all values for variables in
X
≤
j
≤
X
j
.
We now de s c r i be Ne ciporuk's lower bound on formula size. We emphasize that the strength
of the lower bound depends on which partition
X
1
,
X
2
,
...
,
X
p
of the variables
X
is chosen.
After the proof we apply it to the indirect storage access function. The method cannot provide a
lower bound that is larger than
O
(
n
2
/
log
n
)
for a function on
n
variables. (See Problem
9.25
.)
−



















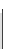















Search WWH ::

Custom Search