Information Technology Reference
In-Depth Information
We emphasize again that subtraction plays a central role in Strassen's algorithm. Without
it we show in Section
10.4
that the standard algorithm is nearly best possible.
Strassen's algorithm is practical for sufficiently large matrices, say with
n
≥
64. It can
also be used to multiply Boolean matrices even though the addition operator (
OR
)andthe
multiplication operator (
AND
)overtheset
B
do not constitute a ring. (See Problem
6.9
.)
6.4 Transitive Closure
The edges of a directed graph
G
=(
V
,
E
)
,
n
=
, specify paths of length 1 between pairs of
vertices. (See Fig.
6.3
.) This information is captured by the Boolean
n
|
V
|
×
n
adjacency matrix
A
=[
a
i
,
j
]
,1
n
,where
a
i
,
j
is 1 if there is an edge from vertex
i
to vertex
j
in
E
and
0 otherwise. (The adjacency matrix for the graph in Fig.
6.3
is given after Lemma
6.4.1
.) Our
goal is to compute a matrix
A
∗
whose
i
,
j
entry
a
i
,
j
has value 1 if there is a path of length
0 or more between vertices
i
and
j
and value 0 otherwise.
A
∗
is called the
transitive closure
of the matrix
A
. The transitive closure function
f
(
n
)
A
∗
≤
i
,
j
≤
n
2
n
2
:
B
→B
maps an arbitrary
n
×
n
n
transitive closure matrix; that is,
f
(
n
)
A
∗
(
A
)=
A
∗
.Inthis
Boolean matrix
A
onto its
n
×
B
section we add and multiply Boolean matrices over the set
using
OR
as the element addition
operation and
AND
as the element multiplication operation. (Note that
(
,0,1
)
is not
a ring; it satisfies all the rules for a ring except for the condition that each element of
B
∨
∧
,
,
B
have
an (additive) inverse under
.)
To c omp u t e
A
∗
we use the following facts: a) the entry in the
r
th row and
s
th column
of the Boolean matrix product
A
2
=
A
∨
A
is 1 if there is a path containing two edges from
vertex
r
to vertex
s
and 0 otherwise (which follows from the definition of Boolean matrix
multiplication given in Section
6.3
), and b) the entry in the
r
th row and
s
th column of
A
k
×
=
A
k−
1
A
is 1 if there is a path containing
k
edges from vertex
r
to vertex
s
and 0
otherwise, as the reader is asked to show. (See Problem
6.11
.)
×
LEMMA
6.4.1
Let
A
be the Boolean adjacency matrix for a directed graph and let
A
k
be the
k
th
power of
A
. Then the following identity holds for
k
≥
1
,where
+
denotes the addition (
OR
)of
Boolean matrices:
+
A
k
(6.2)
Proof
The proof is by induction. The base case is
k
=
1, for which the identity holds.
Assume that it holds for
k
(
I
+
A
)
k
=
I
+
A
+
···
1. We show that it holds for
k
=
K
.Since
(
I
+
A
)
K−
1
=
≤
K
−
2
3
4
1
5
Figure 6.3
A graph that illustrates transitive closure.
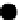











Search WWH ::

Custom Search