Information Technology Reference
In-Depth Information
1
0
q
0
/
0
q
1
/
1
0
1
Start
Figure 4.4
A finite-state machine computing the
EXCLUSIVE OR
of its inputs.
Some examples of regular expressions will clarify the definitions. The regular expression
(
0
+
1
)
∗
denotes the set of all strings over the alphabet
. The expression
(
0
∗
)(
1
)
denotes the strings containing zero or more 0's that end with a single 1. The expression
((
1
)(
0
∗
)(
1
)+
0
)
∗
denotes strings containing an even number of 1's. Thus, the expression
((
0
∗
)(
1
))((
1
)(
0
∗
)(
1
)+
0
)
∗
denotes strings containing an odd number of 1's. This is exactly
the class of strings recognized by the simple DFSM in Fig.
4.4
. (So far we have set in boldface
all regular expressions denoting sets containing letters. Since context will distinguish between
a set containing a letter and the letter itself, we drop the boldface notation at this point.)
Some parentheses in regular expressions can be omitted if we give highest precedence to
Kleene closure, next highest precedence to concatenation, and lowest precedence to union. For
example, we can write
((
0
∗
)(
1
))((
1
)(
0
∗
)(
1
)+
0
)
∗
as 0
∗
1
(
10
∗
1
+
0
)
∗
.
Because regular expressions denote languages, certain combinations of union, concatena-
tion, and Kleene closure operations on regular expressions can be rewritten as other combina-
tions of operations. A regular expression will be treated as identical to the language it denotes.
Tw o
regular expressions are equivalent
if they denote the same language. We now state
properties of regular expressions, leaving their proof to the reader.
{
}
0, 1
THEOREM
4.3.1
Let
∅
and
be the regular expressions denoting the empty set and the set contain-
ing the empty string and let
r
,
s
,and
t
be arbitrary regular expressions. Then the rules shown in
Fig.
4.5
hold.
We illustrate these rules with the following example. Let
a
=
0
∗
1
b
+
0
∗
,where
b
=
c
·
·
10
+
and
c
=(
0
+
10
+
1
)
∗
. Using rule (16) of Fig.
4.5
,werewrite
c
as follows:
c
=(
0
+
10
+
1
)
∗
=(
0
∗
10
+
1
)
∗
0
∗
Then using rule (15) with
r
=
0
∗
10
+
and
s
=
1, we write
b
as follows:
b
=(
0
∗
10
+
1
)
∗
0
∗
10
+
=(
rs
)
∗
r
=
r
(
sr
)
∗
=
0
∗
10
+
(
10
∗
10
+
)
∗
It follows that
a
satisfies
0
∗
1
b
+
0
∗
a
=
·
0
∗
10
∗
10
+
(
10
∗
10
+
)
∗
+
0
∗
=
0
∗
(
10
∗
10
+
)
+
+
0
∗
=
0
∗
((
10
∗
10
+
)
+
+
)
=
0
∗
(
10
∗
10
+
)
∗
=

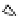







Search WWH ::

Custom Search