Information Technology Reference
In-Depth Information
Fig. 6.5
Bipartite Graph
(Reprinted with permission
from [
10
]. Copyright 2008,
Elsevier Inc.)
2
,
1
,
?
2
,
1
,
0
2
,
0
,
?
1
,
1
,
1
1
,
1
,
?
1
,
1
,
0
between
x
Y
if the value combination
x
can be covered by assigning a
value to cell
y
. The goal is to find a matching that each value combination is linked
to a cell, i.e., a matching in
G
that saturates set
X
.
P. Hall proved the following classical theorem in 1935:
∈
X
and
y
∈
Theorem 6.1
(Hall's Marriage Theorem) Let G be a bipartite graph with partite
sets X and Y . There is a matching in G saturating X iff
|
N
(
S
)
| ≥ |
S
|
for every
is the neighbor set of S which is defined as the set of vertices
adjacent to the vertices in S.
X
has 2
|
X
|
subsets, of which we can only choose a few for pruning. For example,
consider
S
S
⊆
X , where N
(
S
)
=
X
, since
N
(
X
)
≤ |
Y
|
,if
|
Y
|
<
|
X
|
, there is a contradiction.
Example 6.5
Suppose we are processing a column
c
3
of a CA, and
c
3
has 3 cells
unassigned. Assume
t
=
3. Consider 3 columns
c
1
,
c
2
and
c
3
(
c
1
<
c
2
<
c
3
). If
there are three 3-tuple
X
to be covered, then we can
draw the bipartite graph in Fig.
6.5
, where “?” denotes the unassigned cells. Let
Y
be the neighbor set of
X
, obviously
={
2
,
1
,
0
,
1
,
1
,
1
,
1
,
1
,
0
}
|
| =
<
|
| =
Y
2
X
3, so we can not assign these
3 cells to cover
X
.
6.3.7 An Example of the Search Process
Figure
6.6
is an example of the search tree describing the process of constructing
pairwise covering array CA
2
4
. The notation “?” represents an unassigned
cell. We use the SCEH strategy level 1 (i.e.,
SL
(
5
,
,
2
)
1).
The process begins at State I in which the cells of the init-block are assigned. Then
we try to assign possible values to the cells of column 3. The cells ce
4
,
3
and ce
5
,
3
are assigned the value 1 according to SCEH at State II. At State III, two cells ce
5
,
1
and ce
5
,
2
are assigned consecutively to cover all the pairs of the first 3 columns. At
State IV, ce
1
,
4
can only get the value 0 according to LNH. Then there are 2 candidate
values 0 and 1 for ce
2
,
4
. At State V, we assign 0 to ce
2
,
4
. At the next State VI,
if ce
3
,
4
is assigned 0, then according to Marriage Theorem, there are 3 uncovered
combinations of column 3 and 4 (the set
X
), and only 2 unassigned cells left (the set
Y
),
=
. We can not find a match and thus the value 0 for ce
3
,
4
is invalid. So
we assign 1 to ce
3
,
4
and reach State VI. At the State VI, no candidate value for ce
4
,
4
is valid because of Marriage Theorem. So we backtrack to State IV. Similarly, we
also find contradiction at State VIII. At last we find a covering array at State XI. If
we need more than one covering arrays, we can backtrack and continue the search.
|
Y
|
<
|
X
|

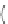



















Search WWH ::

Custom Search