Information Technology Reference
In-Depth Information
a
11
a
12
···
a
1
k
a
11
a
12
···
a
1
k
···
a
11
a
12
···
a
1
k
a
21
a
22
···
a
2
k
a
21
a
22
···
a
2
k
···
a
21
a
22
···
a
2
k
.
.
.
N
rows
···
a
N
1
a
N
2
···
a
Nk
a
N
1
a
N
2
···
a
Nk
···
a
N
1
a
N
2
···
a
Nk
b
11
b
11
···
b
11
b
12
b
12
···
b
12
···
b
1
b
1
···
b
1
b
21
b
21
···
b
21
b
22
b
22
···
b
22
···
b
2
b
2
···
b
2
.
.
.
M
rows
···
b
M
1
b
M
1
···
b
M
1
b
M
2
b
M
2
···
b
M
2
···
b
M
b
M
···
b
M
Fig. 2.5
The product of
A
⊗
B
(Reprinted with permission from [
9
]. Copyright 2008, Elsevier Inc.)
Fig. 2.6
CA
(
N
+
(
v
−
1
)
·
AA
BB
π
v
2
k
M
,
,
3
)
1
2
...
BB
π
BB
π
v
−
1
2.2.2.1 Strength-2 Covering Arrays
For strength
t
2 (i.e., pairwise testing), Stevens and Mendelsohn proved the
following theorem [
8
]:
=
v
k
v
,
Theorem 2.6
(Products of Strength-2 CAs)
If a
CA
(
N
,
,
2
)
and a
CA
(
M
,
2
)
v
k
,
both exist, then a
CA
(
N
+
M
,
2
)
also exists.
v
k
v
,
=
(
a
ij
)
(
,
,
)
=
(
b
ij
)
(
,
)
(
+
Let
A
be CA
N
2
and
B
be CA
M
2
. Then the
N
v
k
,
.
Similarly, there are product methods for pairwise mixed covering arrays. For
details, see [
4
]. The methods can be used recursively.
M
)
×
k
array
C
=
(
c
ij
)
=
A
⊗
B
in Fig.
2.5
is a CA
(
N
+
M
,
2
)
2.2.2.2 Strength-3 Covering Arrays
For covering arrays of strength 3, Chateauneuf and Kreher proved the following
theorem [
1
]:
v
k
v
k
Theorem 2.7
If a
CA
(
N
,
,
3
)
and a
CA
(
M
,
,
2
)
both exist, then a
CA
(
N
+
(
v
−
v
2
k
1
)
·
M
,
,
3
)
also exists.
v
k
v
k
i
Suppose
A
is a CA
(
N
,
,
3
)
, and
B
is a CA
(
M
,
,
2
)
.Let
{
π
|
1
≤
i
≤
v
−
1
}
be the cyclic group of permutations generated by
π
=
(
0
,
1
,...,
v
−
1
)
. In other
i
i
mod
v
.Let
B
π
words,
π
is a bijection that maps symbol
s
to
(
s
+
i
)
be the matrix
i
v
2
k
obtained by applying the permutation
π
to
B
. Then a CA
(
N
+
(
v
−
1
)
·
M
,
,
3
)
can be constructed in the way illustrated in Fig.
2.6
.


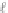


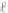


























































Search WWH ::

Custom Search