Information Technology Reference
In-Depth Information
a
b
Duffing chaotic oscillator
Genesio−Tesi chaotic oscillator
4
10
8
3
6
2
4
1
2
0
0
−2
−1
−4
−2
−6
−3
−8
−4
−10
−4
−2
0
2
4
6
−3
−2
−1
0
1
2
3
x1
x1
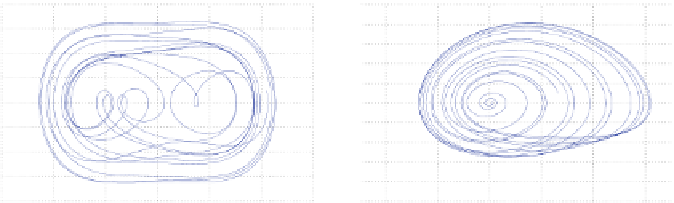
Fig. 9.1
Phase diagram of typical chaotic oscillators (
a
) Duffing's oscillator (
b
) Genesio-Tesi's
oscillator
a description of the oscillator's dynamics in the linear canonical (Brunovsky's)
form is obtained
y
1
y
2
01
00
y
1
y
2
0
1
v
D
C
(9.4)
2. Differential flatness of Genesio-Tesi's oscillator:
By defining the flat output y D x
1
one has x
1
D y, x
2
Dy, x
3
Dy and
y
.3/
Dx
3
D
cy
b y a y C y
2
. Thus all state variables of the Genesio-Tesi
oscillator are expressed as functions of the flat output and its derivatives, and
differential flatness of the oscillator is proven. Moreover, by defining as new
control input
v
D
cy
b y a y C y
2
, and the new state variables y
1
D y,
y
2
Dy, and y
3
Dy a description of the oscillator's dynamics in the linear
canonical (Brunovsky's) form is obtained
0
@
1
A
D
0
@
1
A
0
@
1
A
C
0
@
1
A
v
y
1
y
2
y
3
010
001
000
y
1
y
2
y
3
0
0
1
(9.5)
3. Differential flatness of Chen's oscillator:
By defining the flat output y D x
1
one has x
1
D y, x
2
D
1
a
. yC
ay
/, and x
3
D
y
C
.a
c/y
.2ac
a
2
/y
ay
(for y¤0). From the third row of the associated state-space
equations and after intermediate computations one obtains y
.3/
D.ac C1C
.a
C
c/
y
a
b
b/ yŒ2.2aca
2
/Ca
2
b.aCc/y
ay
2
. yCay/a
2
b.2aca
2
/y.
Thus all state variables of the Chen oscillator are expressed as functions of the
flat output and its derivatives, and differential flatness of the oscillator is proven.
Moreover, by defining as new control input
v
D.acC1Ca
b
b/ yŒ2.2ac
a
2
/Ca
2
b.aCc/y
y
2
.a
C
c/
y
ay
2
. yCay/a
2
b.2aca
2
/y, and the new state
variables y
1
D y, y
2
Dy, and y
3
Dy a description of the oscillator's dynamics
in the linear canonical (Brunovsky's) form is obtained
y
2