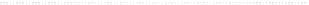Information Technology Reference
In-Depth Information
a
b
15
1
0.9
10
0.8
5
0.7
0.6
0
0.5
−5
0.4
0.3
−10
0.2
−15
0.1
−20
0
−8
−6
−4
−2
0
2
4
6
0
200
400
600
800
1000
1200
1400
1600
1800
2000
x
k (iterations)
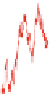
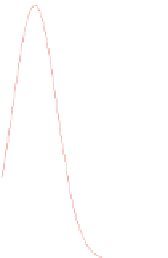
Fig. 7.1
(
a
) Wiener random walk (
b
) Solution of Schrödinger's equation: Shifted Gaussians that
give the probability density function of a stationary diffusion process (
continuous curves
)andthe
approximation of the p.d.f. by symmetric triangular possibility distributions (
dashed lines
)
(or decrements), then according to the CLT it must follow a Gaussian distribution.
Thus one obtains:
Ef
w
.t/gD0 while EŒ
w
.t/ Ef
w
.t/g
2
D
2
t
(7.5)
7.2.3
Outline of Wiener Process Properties
Wiener's process is a stochastic process that satisfies the following conditions:
1.
w
.0/ D 0
2. The distribution of the stochastic variable
w
.t/ is a Gaussian one with a p.d.f.
.x;t/ which satisfies the following relation
@
2
.x;t/
@x
2
;.x;0/D ı.x/
@.x;t/
@t
2
2
(7.6)
D
For a limited number of time instants t
1
<t
2
< <t
n
the stochastic variables
w
.t
j
/
w
.t
j1
/ are independent.
3. It holds that Ef
w
.t/gD0 and EfŒ
w
.t/
w
.s/
2
D
2
.t s/g for all 0st.
4.
w
.t/ is a continuous process
The standard Wiener process evolves in time according to the following relation
p
hN.0;1/
(7.7)
w
.t C h/ D
w
.t/ C
The Wiener process actually describes a diffusion phenomenon and the associated
p.d.f. of stochastic variable is given by
p
2t
e
x
2
1
.x;t/ D
(7.8)
2t