Image Processing Reference
In-Depth Information
Cluster β
i
Crisp Lower
Approximation
A( )
β
i
with
µ
ij
= 1
Fuzzy
Boundary
B( )
β
i
with
µ
ij
[0, 1]
RFCM: cluster
β
i
is represented by crisp lower bound and fuzzy boundary
FIGURE 2.1
2.3.2 Cluster Prototypes
The new centroid is calculated based on the weighting average of the crisp lower approxi-
mation and fuzzy boundary. Computation of the centroid is modified to include the effects
of both fuzzy memberships and lower and upper bounds. The modified centroid calculation
for the RFCM is obtained by solving Equation 2.4 with respect to v
i
:
8
<
:
w×C
+ w×D
if A(β
i
) =∅, B(β
i
) =∅
1
1
v
RF
i
=
C
if A(β
i
) =∅, B(β
i
) =∅
(2.5)
1
D
1
if A(β
i
) =∅, B(β
i
) =∅
|A(β
i
)|
x
j
∈A(β
i
)
1
C
1
=
x
j
;
where|A(β
i
)|represents the cardinality of A(β
i
)
n
i
x
j
∈B
n
i
=
x
j
∈B
1
(
ij
)
´m
x
j
;
(
ij
)
´m
andD
=
where
1
(
β
i
)
(
β
i
)
Thus, the cluster prototypes (centroids) depend on the parameters w and w, and fuzzifica-
tion factor m rule their relative influence. The correlated influence of these parameters and
fuzzification factor, makes it somewhat di
cult to determine their optimal values. Since
the objects lying in lower approximation definitely belong to a cluster, they are assigned
a higher weight w compared to w of the objects lying in boundary region. Hence, for the
RFCM, the values are given by 0 < w < w < 1.
From the above discussions, the following properties of the RFCM algorithm can be
derived.
1.
A(β
i
) = U , U be the set of objects of concern.
2. A(β
i
)∩A(β
k
) =∅,∀i = k.
3. A(β
i
)∩B(β
i
) =∅,∀i.
4.∃i, k, B(β
i
)∩B(β
k
) =∅.
5.
ij
= 1,∀x
j
∈A(β
i
).
6.
ij
∈[0, 1],∀x
j
∈B(β
i
).
Let us briefly comment on some properties of the RFCM. The property 2 says that if an
object x
j
∈A(β
i
)⇒x
j
/∈A(β
k
),∀k = i. That is, the object x
j
is contained in β
i
definitely.
The property 3 establishes the fact that if x
j
∈A(β
i
)⇒x
j
/∈B(β
i
), - that is, an object
may not be in both lower and boundary region of a cluster β
i
. The property 4 says that

















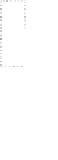









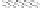






















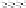


















Search WWH ::

Custom Search