Image Processing Reference
In-Depth Information
Peters, 2009a,b). Let Z = X∪Y and let the notation
[z
/
∼
=
B
]
X
={z∈z
/
∼
=
B
|z∈X},
denote the portion of the tolerance class z
/
∼
=
B
that belongs to X, and similarly, use the
notation
[z
/
∼
=
B
]
Y
={z∈z
/
∼
=
B
|z∈Y},
to denote the portion that belongs to Y . Further, let the sets X and Y be weakly near each
other using Defn. 2. Then, a NM between X and Y is given in (Henry and Peters, 2009a,b)
by
=
B
(X,Y ) =
=
B
|
!
−1
X
X
=
B
|
min(|[z
∼
=
B
]
X
|,|[z
∼
=
B
]
Y
|)
NM
∼
|z
∼
|z
∼
(7.3)
max(|[z
∼
=
B
]
X
|,|[z
∼
=
B
]
Y
|)
z
∼
=
B
∈Z
∼
=
B
z
∼
=
B
∈Z
∼
=
B
The idea behind Eq. 7.3 is that similar sets should contain a similar number of objects in
each tolerance class. Thus, for each tolerance class obtained from Z = X∪Y , Eq. 7.3 counts
the number of objects that belong to X and Y and takes the ratio (as a proper fraction)
of their cardinalities. Furthermore, each ratio is weighted by the total size of the tolerance
class (thus giving importance to the larger classes) and the final result is normalized by
dividing by the sum of all the cardinalities. The range of Eq. 7.3 is in the interval [0,1],
where a value of 1 is obtained if the sets are equivalent and a value of 0 is obtained if they
have no elements in common.
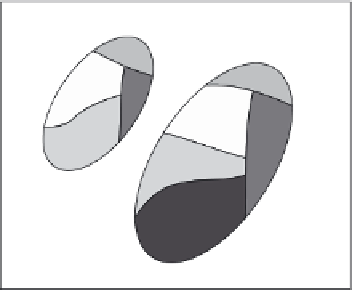
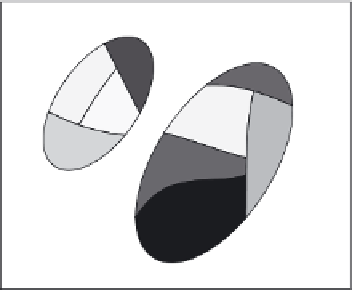
As an example of the degree of nearness between two sets, consider Fig. 7.3 in which each
image consists of two sets of objects, X and Y . Each color in the figures corresponds to
an elementary set where all the objects in the class share the same description. The idea
behind Eq. 7.3 is that the nearness of sets in a perceptual system is based on the cardinality
of the classes that they share. Thus, the sets in Fig. 7.3a are closer (more near) to each
other in terms of their descriptions than the sets in Fig. 7.3b.
(7.3a) Sample low degree of nearness
(7.3b) Sample high degree of nearness
FIGURE 7.3: (See color insert) Examples of degree of nearness between two sets: (a) High
degree of nearness, and (b) low degree of nearness (Henry and Peters, 2009a).



Search WWH ::

Custom Search