Intuitionistic Fuzzy Clustering Algorithms - Intuitionistic Fuzzy Aggregation and Clustering - page 200

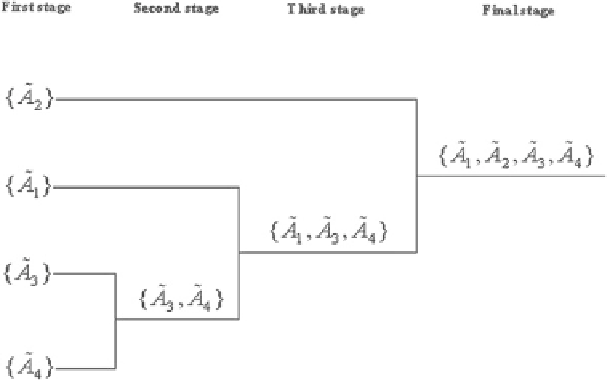
Fig. 2.2 Classification of the enterprises A j ( j = 1 , 2 , 3 , 4 )

μ R : X × Y →[ 0 , 1 ] , v R : X × Y →[ 0 , 1 ] (2.114)

and

≤ μ R ( , ) +

v R (

, ) ≤ , ( , ) ∈ ×

0 x y x y 1 for any x y X Y (2.115)

Definition 2.17 (Bustince 2000) Let R be an intuitionistic fuzzy relation. If

(1) ( Reflexivity ). μ R ( x , x ) = 1 , v R ( x , x ) = 0, for any x ∈ X .

(2) ( Symmetry ). μ R ( x , y ) = μ R ( y , x ), v R ( x , y ) = v R ( y , x ) , for any ( x , y ) ∈ X × Y ,

then R is called an intuitionistic fuzzy similarity relation.

Definition 2.18 (Xu et al. 2011) Let α = (α 1 ,α 2 ,...,α n ) be a vector. If all α i =

(μ α i , v )( i = 1 , 2 ,..., n ) are IFVs, then we call α an intuitionistic fuzzy vector,

α i

T as the transpose of T

and denote α α , where α is a n -dimensional column vector.

Definition 2.19 (Xu et al. 2011) Let α, β ∈ X 1 × n , where X 1 × n denotes the set of

intuitionistic fuzzy vectors. Then

α · β = ( max { min { μ α i ,μ β i }} , min { max { v α i , v β j }} )

n
∨

n
∧ = (

1 (μ α i ∧ μ β i ), 1 (

v

α i ∨

v

β j ))

(2.116)

i = i =

is called the inner product of α and β , where ∨ and ∧ denote the max and min

operations respectively.

Definition 2.20 (Xu et al. 2011) Let α, β ∈ X 1 × n , if α · β = ( 0 , 1 ) or ( 0 , 0 ) . Then

we call that α is orthogonal to β .