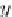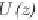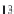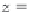Geoscience Reference
In-Depth Information
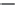
Figure 3.1 Steady turbulent channel flow and its profiles of mean velocity
U
and
mean kinematic shear stress
T
13
.
as well. We can then write
U
i
, and in steady conditions the
ensemble-averaged momentum
equation (3.6)
reduces to
=[
U(z),
0
,
0
]
∂
2
U
i
∂x
j
∂x
j
.
∂x
j
u
i
u
j
=−
∂
1
ρ
∂P
∂x
i
+
ν
(3.9)
This expresses a balance among the turbulent stress divergence, the mean pres-
sure gradient, and the viscous stress divergence. The homogeneity in
y
makes that
component equation vanish, so we have
uw
∂
∂z
ν
∂U
∂z
1
ρ
∂P
∂x
.
i
=
1:
−
=−
(3.10)
∂w
2
∂z
=−
1
ρ
∂P
∂z
.
i
=
3:
(3.11)
By differentiating
Eq. (3.11)
with respect to
x
, using homogeneity, and changing
the order of differentiation we conclude that
∂w
2
∂z
=
∂
∂x
1
ρ
∂
∂x
∂P
∂z
=−
1
ρ
∂
∂z
∂P
∂x
,
0
=−
(3.12)
which implies that
∂P /∂x
does not depen
d on
z
.
Equation (3.10)
then implies that
the mean kinematic shear stress
T
13
=−
+
ν∂U/∂z
varies linearly with
z
,as
sketched in
Figure 3.1
.
As we showed through
Eq. (3.8)
, the viscous part of the
shear stress is negligible except very near the walls.
uw