Related Work - Hierarchical Neural Networks for Image Interpretation - page 59

dark regions of facial images, such as the eyes and the shadow of the nose. The
figure also shows the encoding h of a face and its reconstruction. Because both the
weights and the coefficients of h contain a large number of vanishing components,
the encoding is sparse. The reason for this is that the model is only allowed to add
positively weighted non-negative basis-vectors to the reconstruction. Thus, different
contributions do not cancel out, as for instance in principal components analysis.
Although the generative model is linear, inference of the hidden representation
h from an image v is highly non-linear. The reason for this is the non-negativity
constraint. It is not clear how the best hidden representation could be computed
directly from W and v . However, as seen above, h can be computed by a simple
iterative scheme. Because learning of weights should occur on a much slower time-
scale than this inference, W can be regarded as constant. Then only the update-
equations for H remain. When minimizing k v − Wh k 2 , h is sent in the top-down
direction through W. Wh has dimension n and is passed in the bottom-up direction
through W T . The resulting vector W T Wh has the same number r of components
as h . It is compared to W T v , which is the image v passed in the bottom-up direction
through W T . The comparison is done by element-wise division yielding a vector of
ones if the reconstruction is perfect: v = Wh. In this case, h is not changed.
When minimizing D ( v k Wh ) , the similarity of v and its top-down reconstruc-
tion Wh is measured in the bottom-layer of the network by element-wise division
v i / ( Wh ) i . The n -dimensional similarity-vector is passed in the bottom-up direc-
tion through W T , yielding a vector of dimension r . Its components are scaled down
with the element-wise inverse of the vector of ones passed through W T to make the

update factors for h unity if the reconstruction is perfect.
This scheme of expanding the hidden representation to the visible layer, mea-
suring differences to the observations in the visible layer, contracting the deviations
to the hidden layer, and updating the estimate resembles the operation of a Kalman
filter [116]. The difference is that in a Kalman filter deviations are measured as
differences and update is additive, while in the non-negative matrix factorization
deviations are measured with quotients and updates are multiplicative. Because the
optimized function is convex for a fixed W , the iterative algorithm is guaranteed to
find the optimal solution.

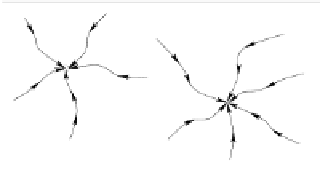
Learning Continuous Attractors. In most models of associative memories, pat-
terns are stored as attractive fixed points at discrete locations in state space, as

(a) (b)

Fig. 3.17. Representing objects by attractors: (a) discrete attractors represent isolated patterns;
(b) continuous attractors represent pattern manifolds (images after [209]).