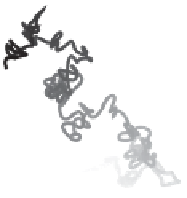Database Reference
In-Depth Information
Figure 15.1 Some examples of Brownian motions.
random walkers tend to travel roughly the same distance between sightings.
However, there are situations in which equations for Brownian motion are no
longer applicable. An example occurs if the jumps are of very large distances:
this is the case for some animal movements. Measurements on albatrosses,
monkeys, and marine predators suggested that animal trajectories are different
from the Brownian motion, and they are better approximated by the so-called
Levy flight
. The French mathematician Paul Levy investigated in the 1930s the
mathematics of random walks with infinite moments. A random walk of
N
steps
is a sum of
N
independent and identically distributed random variables with
mean
μ
=
0 and variance
σ
2
, that is,
S
N
=
X
1
+
X
2
+···+
X
N
.Levy posed
the following question: when does the probability distribution
P
N
(
x
) of the sum
of
N
steps have a similar form as the probability distribution of a single step
p
(
x
)? For walks with finite jump variances, the central limit theorem implies
that the overall probability
P
N
(
x
) is Gaussian. For infinite variance random
walks, the Fourier transform of
p
(
x
)hastheform
p
(
k
)
=
e
−|
k
|
β
with
β<
2.
The Gaussian distribution (Brownian motion case) corresponds to
β
=
2, and
the Cauchy distribution corresponds to
β
=
1. Therefore, Levy flights are a
generalization of Brownian motions (Figure
15.2
).
When the absolute value of
x
is large,
p
(
x
) is approximately
|
x
|
−
(1
−
β
)
,which
implies that the second moment of
p
(
x
) is infinite when
β<
2. This means that
there is no characteristic size for the random walk jumps, except in the Gaussian
case of
β
=
2. It is just this absence of a characteristic size that makes Levy
random walks scale-invariant fractals.