Neural Networks: An Overview - Neural Networks: Methodology and Applications - page 18

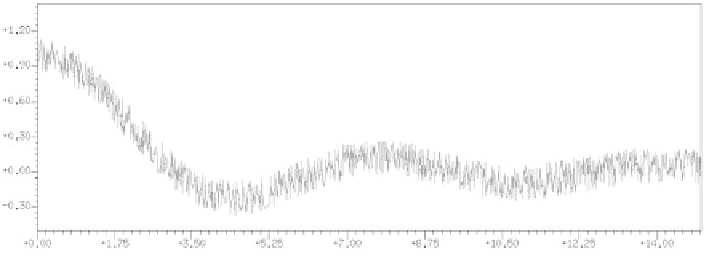
Fig. 1.10. A quantity to be modeled

training is a procedure whereby the least squares cost function is minimized,
so as to find an appropriate weight vector w 0 .
That procedure suggests two questions, which are central in any neural
network application, i.e.,

• for a given architecture, how can one find the neural network for which

the least squares cost function is minimal?

• if such a neural network has been found, how can its prediction ability be

assessed?

Chapter 2 of the present topic will provide the reader with a methodology,
based on first principles, which will answer the above questions.
These questions are not specific to neural networks: they are standard
questions in the field of modeling, that have been asked for many years by all
scientists (engineers, economists, biologists, and statisticians) who endeavor to
extract relevant information from data [Seber 1989; Antoniadis 1992; Draper
1998]. Actually, the path from function approximation to parameter estima-
tion of a regression function is the traditional path of any statistician in search
of a model: therefore, we will take advantage of theoretical advances of sta-
tistics, especially in regression.
We will now summarize the steps that were just described.

• When a mathematical model of dependencies between variables is sought,

one tries to find the regression function of the variable of interest, i.e., the
function that would be obtained by averaging, at each point of variable
space, the results of an infinite number of measurements; the regression
function is forever unknown. Figure 1.10 shows a quantity y p ( x )thatone
tries to model: the best approximation of the (unknown) regression func-
tion is sought.

• A finite number of measurements are performed, as shown on Fig. 1.11.

• A neural network provides an approximation of the regression function if

its parameters are estimated in such a way that the sum of the squared