Modeling with Neural Networks: Principles and Model Design Methodology - Neural Networks: Methodology and Applications - page 116

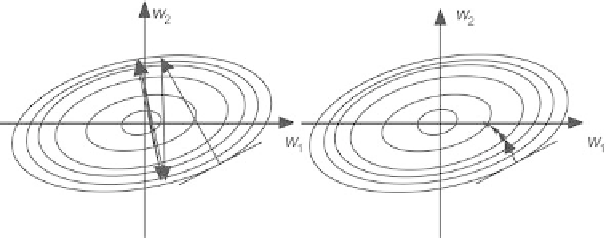
Fig. 2.7. Minimization of the cost function by simple gradient descent

illustrated on Fig. 2.7, which shows the iso-cost lines of the cost function
(depending on two parameters w 1 and w 2 ), and the variation of vector w
during the minimization.

• In the vicinity of a minimum of the cost function, the gradient becomes

very small, so that the variation of the parameters becomes extremely
slow; the situation is similar if the cost function has plateaus, so that,
when training becomes very slow, there is no way to tell whether that is
due to a plateau that may be very far from a minimum, or whether that
is due to the presence of a real minimum.

• If the curvature of the surface is very nonisotropic, the direction of the

gradient may be very different from the direction of the location of the
minimum; such is the case if the cost surface has long narrow valleys as
shown on Fig. 2.7.

In order to overcome the first drawback, a large number of heuristics were
suggested, with varied success rates. Line search techniques (as discussed in
the additional material at the end of the chapter) have solid foundations and
are therefore recommended.
In order to overcome the other two di culties, second-order gradient meth-
ods must be used. Instead of updating the parameters proportionally to the
gradient of the cost function, one can make use of the information contained
in the second derivatives of the cost function. Some of those methods also
make use of a parameter µ whose optimal value can be found through line
search techniques.
The most popular second-order techniques are described below.

Second-Order Gradient Methods

All second-order methods are derived from Newton's method, whose principle
is discussed in the present section.
The Taylor expansion of a function J ( w ) of a single variable w in the
vicinity of a minimum w ∗ is given by