PerformingNon-Rigid Structure fromMotion - Deformable Surface 3D Reconstruction from Monocular Images - page 71

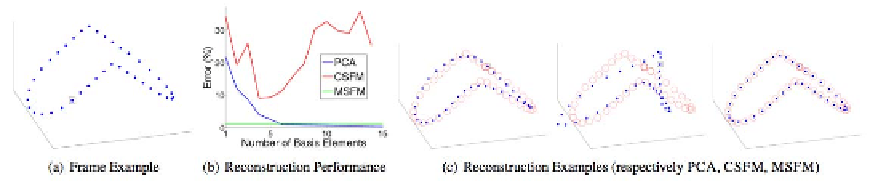
Figure 6.10: Comparison of NRSFM using a locally smooth manifold representation of the shape
space Rabaud and Belongie [ 2008 ] (MSFM) with a classical NRSFM method (CSFM) Torresani et al.
[ 2008 ] and with PCA learned from known 3D shapes. Note that the method of Rabaud and Belongie
[ 2008 ] is better adapted to cope with this non-smooth deformation of a circular shape. Courtesy of V.
Rabaud. © 2008 IEEE.
Figure 6.11: Quadratic deformation modes applied to a synthetic planar patch Fayad et al. [ 2009 ].
Courtesy of A. Del Bue.
especially since existing methods are only reliable when using a small number of basis shapes.
Recently, two publications have advocated the use of alternative models to capture more complex
deformations. The first one Rabaud and Belongie [ 2008 ] exploits the concept of locally smooth
manifold learning (LSML) Dollar et al. [ 2007 ]. As suggested by Fig. 6.9 , this relaxes the implicit
constraint that the shapes lie on a linear subspace. Instead of optimizing basis shapes and their
coefficients, the 3D coordinates of the object's points are optimized directly, and the resulting shapes
are regularized to form a locally smooth manifold. This is done in an iterative manner. At each
iteration, the manifold is learned from the current shape estimates. This yields a gradient for the
LMSL error term, which is combined with a gradient computed from a temporal smoothness term
explained in Section 6.2 . As shown in Fig. 6.10 , this approach has proved particularly well-adapted
to model large deformations that do not lie on linear manifolds, and therefore cannot be captured
by a linear subspace.
The second approach Fayad et al. [ 2009 ] to replacing the linear subspace model with a higher-
order one exploits a quadratic deformation model, which was originally introduced in the Computer
Graphics community for simulation purposes Müller et al. [ 2005 ]. In this case, the shape of a set of