Image Processing Reference
In-Depth Information
(a)
(b)
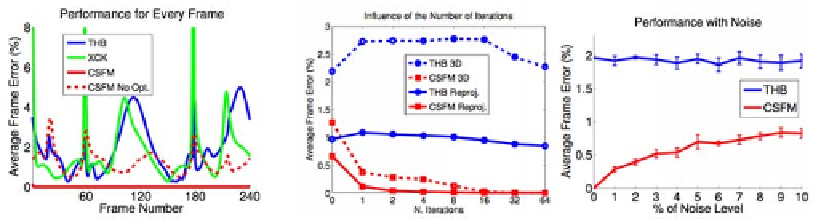
Figure 6.3:
Comparison of the results of
Rabaud and Belongie
[
2009
](CSFM) with those of
Xiao
et al.
[
2004b
](XCK) and
Torresani
et al.
[
2008
](THB) on the shark data. (a) Reconstruction error for all frames
in the sequence. (b) For a single frame, convergence speed and reconstruction error as a function of noise.
Errors are given as mean distances between the reconstructed points and their true location, divided by
the span of the true shape. Courtesy of V. Rabaud.
Of course, this measure cannot be directly computed, since it depends on the 3D shapes, which are
unknown. However, its infimum and supremum can be obtained from the measurement matrix
W
.
This is used to build a set of pairs of triplets
F
={
((i, j, k), (i
,j
,k
))
|
a
F
(i,j,k)
≤
a
F
(i
,j
,k
)
}
,
which implicitly defines an ordering of triplets based on the similarity measure. Furthermore, it can
be shown that
a
F
is related to the values of the shape coefficients, such that
2
.
1
3
c
i
c
j
2
c
i
c
k
2
c
j
c
k
2
a
F
(i,j,k)
=
−
2
+
−
2
+
−
(6.11)
Therefore, the relations in set
can be used to define constraints in a Generalized Non-metric Multi-
Dimensional Scaling problem
Agarwal
et al.
[
2007
] written as a semi-definite program (SDP). Solv-
ing this SDP yields an estimate of the shape coefficients
c
in each frame. Given the shape coefficients,
the shape basis and rotations are then computed. Fig.
6.3
compares the reconstruction accuracy
of
Rabaud and Belongie
[
2009
] with other methods on the shark dataset. The reconstruction errors
are given as mean distances between the reconstructed points and their true location, divided by the
span of the true shape. Note that the method of
Rabaud and Belongie
[
2009
] converges quickly and
yields better accuracy than the other approaches.
While the zeroth order motion model and the shape repetition assumption are very helpful,
they both have their shortcomings. The former usually does not really apply to the true dynamics
of a deformable surface, and the latter requires having long enough sequences such that the same
shape appears several times. Furthermore, in the above-mentioned works, temporal consistency was
not sufficient to fully constrain reconstruction. As a consequence, the resulting techniques had to
exploit additional geometric constraints, as described in Section
6.3
.
F
Search WWH ::

Custom Search