Image Processing Reference
In-Depth Information
1.4
0.7
QO
QP
SOCP
QO
QP
SOCP
1.2
0.6
1
0.5
0.8
0.4
0.6
0.3
0.2
0.4
0.2
0.1
0
0
0
50
100
150
200
250
300
350
0
50
100
150
200
250
300
350
frame #
frame #
Figure 4.5:
Comparison of the accuracies obtained with the SOCP formulation based on
Salzmann
et al.
[
2007a
] with the QP and unconstrained (QO) formulations of
Zhu
et al.
[
2008
]. Reconstructions were
obtained with image noise variance 1 (left) and 2 (right). Note that the QP and QO approaches yield
better results than the SOCP one. Courtesy of J. Zhu.
4.2
IMPOSINGGEOMETRICCONSTRAINTS
The methods discussed in the previous section are very generic in that they make very few assumptions
on the smoothness or physical properties of the surface. However, they are all limited by the fact
that they involve frame-to-frame tracking and are therefore subject to drift and irrecoverable failure
if there are too few valid correspondences in any given frame. Furthermore, they require a full video
sequence, as well as an initial shape estimate for the first frame, either of which may not be available.
A useful alternative is therefore to replace temporal consistency constraints by geometric
ones that allow reconstruction using a single input image or a very short sequence of consecutive
ones. The difficulty then is to design the constraints so as to make as few unwarranted assumptions
on the allowable surface deformations as possible. In the remainder of this section, we classify
approaches according to how stringent the constraints are. We start with developable surfaces, whose
deformations are very strongly constrained. We then move on to surfaces that deform smoothly,
including those that remain globally smooth and those that need only be locally smooth and can
therefore develop creases. We conclude by discussing inextensible surfaces.
4.2.1 DEVELOPABLE SURFACES
Developable surfaces are surfaces with zero Gaussian curvature, meaning that, for all points and
all possible deformations, one of the principal curvatures must be zero. Such 3D surfaces can be
flattened onto a plane without distortion and are ruled surfaces. For example, initially flat pieces of
paper are developable and are often used to demonstrate techniques that rely on this property.
As shown in
Gumerov
et al.
[
2004
], given only surface boundaries in both the reference and
input image acquired by a calibrated camera, it is possible to recover the 3D structure by solving
Ordinary Differential Equations. Another approach is to explicitly parameterize the reference surface






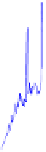





















































































































































































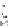







































































































































































































































































































































































































Search WWH ::

Custom Search