Image Processing Reference
In-Depth Information
t+1
v
j
t
v
j
~
v
t+1
v
t
t+1
v
i
Figure 4.3:
The orientation of the edge between
v
i
and
v
j
at time
t
+
1 is predicted to be the same as
at time
t
. The distance between the true vertex
v
t
+
1
j
v
t
+
1
j
and its prediction
˜
is then constrained to be less
than some specified value.
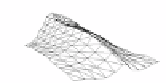
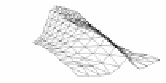
Figure 4.4:
Recovering the deformations of a plastic bag with a sharp crease in it from an 86-frames
video using the
Salzmann
et al.
[
2007a
] method. © 2007 IEEE.
where
l
i,j
is the original length of the edge between vertices
i
and
j
, and
λ
encodes the amount of
possible motion. These temporal constraints have the advantage of being more realistic than the ones
of Eq.
4.2
and can handle highly-deformable surfaces such as the one of Fig.
4.4
without adding
unwarranted smoothness. It was later shown that the resulting problem could be reformulated as an
unconstrained quadratic optimization problem, which is even easier to solve
Zhu
et al.
[
2008
]. To
this end, the SOCP correspondence constraints of the problem in Eq.
4.4
are turned into equalities
by introducing one slack variable for each correspondence. The sum of these slack variables can then
be expressed as a quadratic function of the shape, and directly minimized in the objective function.
The edge orientation constraints are either kept as constraints to yield a QP problem, or re-written
as a quadratic regularizer, thus resulting in an unconstrained optimization problem. Fig.
4.5
depicts
the reconstruction error of these two formulations, and compares them against the results of the
SOCP approach. The reconstruction error is given as the mean vertex-to-vertex distance between
ground-truth and the recovered surface.

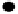














































Search WWH ::

Custom Search