PerformingTemplate-Based Reconstruction - Deformable Surface 3D Reconstruction from Monocular Images - page 30

1400 1400

1200 1200

1000 1000

800 800

600 600

400 400

200 200

0 0

0 200 400 600 800 1000 1200 1400 0 200 400 600 800 1000 1200 1400

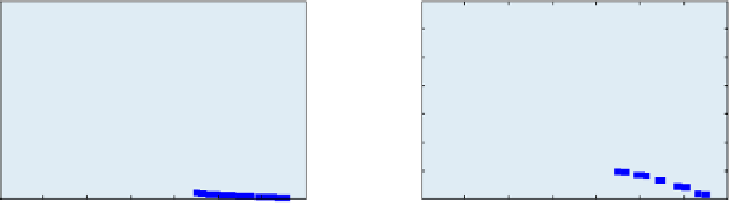
Figure 4.1: Singular values for a 5 frames sequence under perspective projection based on Salzmann et al.
[ 2007b ]. Left: Without temporal consistency constraints between frames, the linear system is ill-
constrained. Right: Bounding the frame-to-frame displacements transforms the ill-conditioned linear
system into a well-conditioned one. The smaller singular values have increased and are now clearly non-
zero. Since our motion model introduces more equations than strictly necessary, the other values are also
affected, but only very slightly.

4.1 IMPOSINGTEMPORAL CONSISTENCY

When dealing with video sequences, one can assume that the surface does not move randomly be-
tween consecutive frames, whatever its physical properties. One way to overcome the rank deficiency
of the matrix of Eq. 4.1 is therefore to perform the reconstruction over several frames simultaneously.
This amounts to stacking the coordinate vectors x of Eq. 4.1 , one for each time frame, and creating
a block diagonal matrix whose elements are matrices M , again one for each time frame. Without
temporal constraints to link the coordinate vectors across frames, this system is just as ill-conditioned
as before. However, because displacement speeds are limited, the range of frame-to-frame motion
is always bounded, which can be expressed as a set of additional linear constraints of the form

x t − 1 x t

− = ≤ t ≤ N f ,

0 , 2 (4.2)

where x t is the coordinate vector for frame t and N f is the total number of frames. These constraints
link the coordinate vectors and can be added to the correspondence equations in the joint system for
all N f frames. The resulting linear system is much better-conditioned as depicted by Fig. 4.1 . Since
this system is solved in the least-squares sense, the motion equations will not be truly enforced, and
thus some motion will be allowed. As a result, given the shape at the beginning and at the end of
a sequence, the surface can be simultaneously reconstructed over the whole sequence as shown in
Fig. 4.2 .
These simple temporal constraints, however, do not accurately model the true dynamical
behavior of a non-rigid surface and, as a result, the reconstructions are not necessarily very accurate.
Furthermore, as discussed above, solving the linear system of Eq. 4.1 in the least-squares sense is
not strictly equivalent to minimizing the true reprojection error. In Salzmann et al. [ 2007a ], this was
remedied by exploiting techniques proposed for rigid object modeling Kahl [ 2005 ], Ke and Kanade