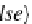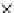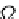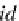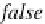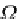Database Reference
In-Depth Information
Show that for any two logic values (i.e., closed objects)
f,
g
∈
L
DB
, for any
(f,
T(f
two morphisms
f,g
:
Υ
→
Ω
, their logic disjunction
T
∪
g)
=
∪
g)
is
equal to the information flux of the arrow
◦
:
→
Ω
.
6. Based on the points 4 and 5 above, we conclude that the basic and derived truth-
values are expressed by the homset
DB
(Υ,Ω)
, with bottom arrow
false
f,g
Υ
:
Υ
→
Ω
and top arrow
true
:
Υ
→
Ω
, and hence, dually, by their information fluxes
DB
(Υ,Ω)
=
Ob
DB
sk
={
f
Ob
DB
sk
pro-
vided by Lemma
19
. By reduction to simple databases, we obtain the complete
sublattice of truth-values
|
f
∈
DB
(Υ,Ω)
}
, with the bijection
β
:
L
DB
=
(Ob
DB
sk
,
,
⊗
,
⊕
)
=
(Ob
DB
sk
,
⊆
,
∩
,T
∪
)
⊂
L
DB
in Definition
63
. Why can't we simply extend this lattice by the standard nega-
tion operator (i.e., the set difference
Υ
\
_) and hence obtain a Boolean algebra
for the standard propositional logic?
7. How did we define, based on the Birkhoff polarity over the complete infini-
tary distributive lattice
(W,
≤
,
∧
,
∨
,
0
,
1
)
, a Dedekind-McNeile closure oper-
ator and the autoreferential Kripke-like semantics for such lattices? Why is it
interesting for us to consider the negation operators which can be derived by the
Birkhoff polarity from the incompatibility relations equal to partial orders? We
obtained a homomorphism
Γ
F
(W)
between the standard Heyting
algebras, whose elements are the set of the hereditary subsets of
W
denoted by
H(W)
, and the Heyting algebras of
closed
hereditary subsets
:
H
(W)
→
H(W)
.
Why do we need to work with this second, that is, the closed version of Heyting
algebras?
8. Why can't the “vectorization” operation _
.
which transforms each database in-
stance
A
into an unary relation
A
be used in order to have an observationally
equivalent relation of a given database, such that
T(
{
A
}
)
=
TA
?Forwhich
strict subclass of the database mapping systems is such an equivalence still
valid? What are the fundamental properties of the mapping
F
(W)
⊆
Υ
introduced in Proposition
69
, and in which way can we represent any closed
object
TA
in the
DB
category from the relation
:
Ob
DB
→
(A)
?
9. The weak monoidal topos database logic WMTL is defined by a strict subclass
of the Heyting algebras. Why can we consider this weak monoidal topos logic
as an abstract-behavior logic? In which way do we provide an embedding of
WMTL into the intuitionistic propositional bimodal logics, and how can we
translate the closure operator
Γ
(analogous to the database power-view operator
T
) obtained from Dedekind-McNeile Galois connection? What is the Gödel-
like translation from WMTL into the S4 extended bimodal logic? By using