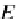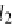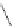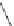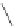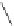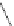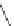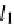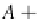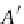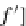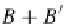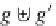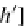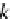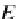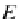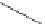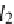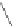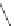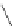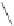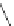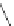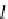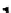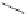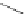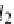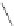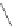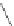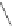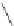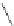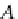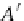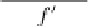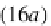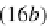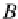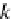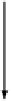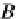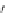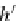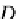Database Reference
In-Depth Information
=
1
≤
j
≤
m
A
j
,m
1,
A
=
1
≤
j
≤
m
A
j
,m
≥
=
1
≤
i
≤
k
B
i
,k
Let
A
≥
1,
B
≥
1 and
B
=
1
≤
i
≤
k
B
i
,k
≥
l
1
1. Let
l
:
E
→
B
be the subset of ptp arrows in
such that
the codomain of each of these ptp arrows is an object in
B
i
,
1
≤
i
≤
k
, and let
B
be the subset of ptp arrows in
l
1
l
:
→
E
such that the codomain of each of these
ptp arrows is an object in
B
i
,
1
≤
i
≤
k
. Then
l
1
=
l,l
, and hence we obtain two
commutative diagrams:
so that, from the fact that by hypothesis both diagrams (16a) and (16b) are the
pullbacks diagrams, we have the unique arrows
e
:
E
→
A
such that
l
=
g
◦
e
,
e
, and
e
:
A
such that
l
=
g
◦
e
,
l
2
=
f
◦
e
. Consequently,
l
2
=
f
◦
E
→
e,e
:
A
such that
l
1
=
l,l
=
there is a unique arrow
e
1
=
E
→
A
+
g
◦
e,g
◦
e
=
g
)
e,e
=
g
)
e,f
◦
e
(g
◦
(g
◦
e
, and
l
2
=
f
◦
(from the
T(f
∪
f
◦
T(l
2
∪
l
2
)
Tl
2
=
l
2
), so that
fact that
f
◦
e,f
◦
e
=
◦
e
e
)
=
=
e,f
◦
e
=[
f,f
]◦
e,e
=[
f,f
]◦
l
2
=
f
◦
e
. Consequently, diagram (16)
is a pullback diagram.
Claim 2. Let us show it for the pullback diagram
A
g
B
composed
by the simple arrows. Then, form the proof of Proposition
48
in Sect.
8.1.3
,the
pullback object is
LimP
f
C
\
f))
∩
f)
=
((T A
∩
g)
∪
(T A
×
((T B
∪
(T B
\
g))
with two
B
where
p
A
p
A
,
1
1
,p
B
monic cone arrows,
[
⊥
]:
LimP
→
A
and
[⊥
]:
LimP
→
=
\
f))
and
p
B
∩
f)
T ((T A
∩
g)
∪
(T A
=
T ((T B
∪
(T B
\
g))
.If
f
:
A
C
is epic
TC
. Thus,
p
B
then
f
∩
f)
=
=
T ((T B
∪
(T B
\
g))
=
T ((T B
∩
TC)
∪
(T B
\
g))
=
]
p
B
1
,p
B
TB
(from the fact that
g
⊆
(T B
∩
TC)
). Consequently,
[⊥
=
TB
, and