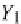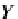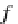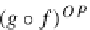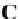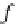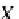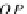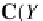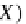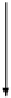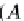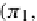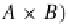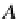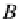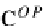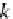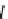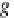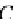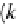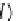Database Reference
In-Depth Information
The Yoneda lemma is one of the most famous basic results of category theory. It
describes representable functors in functor categories. The Yoneda embedding for
any given category
C
is given by the covariant functor
H
Set
C
OP
:
C
→
such that,
C
OP
(X,
_
)
for any object
X
in
C
, we obtain the contravariant hom-functor
h
X
=
:
C
OP
Set
.
Consequently, for any object
Y
in
C
OP
,
h
X
(Y
1
)
→
C
OP
(X,Y
1
)
, while for any
=
arrow
f
OP
:
Y
1
→
Y
2
in
C
OP
, we obtain the arrow (function) in
Set
,
h
X
(f
OP
)
:
C
OP
(X,Y
1
)
C
OP
(X,Y
2
)
is a composition with
f
OP
, i.e., for any
g
OP
→
:
X
→
Y
1
in
C
OP
(X,Y
1
)
we obtain the arrow
h
X
(f
OP
)(g
OP
)
=
f
OP
◦
g
OP
=
(g
◦
f)
OP
:
Y
2
, such that the following diagram commutes in
C
OP
(or, dually in
C
):
X
→
In the case when
f
OP
Y
2
in
C
OP
:
Y
1
→
is a
universal arrow
, the function
h
X
(f
OP
)
:
C
OP
(X,Y
2
)
(an arrow in
Set
) is a bijection.
Let us consider two significant cases of Yoneda embedding for categorial
prod-
ucts
and
coproducts
(without the necessity to introduce the more general case of
limits and colimits):
1. The universal arrows for the
products f
OP
C
OP
(X,Y
1
)
→
=
(π
1
,π
2
)
:
(A
×
B,A
×
B)
(A,B)
in
C
OP
C
OP
, where
π
1
:
=
D
×
D
, and a given object
X
=
(C,C)
∈
×
A
,
π
2
:
×
A
B
are two epimorphisms in
D
corresponding to the
first and second projections, respectively. Thus we obtain the following case for
the commutative diagram above in
C
OP
B
A
B
=
×
D
D
(and its corresponding commu-
tative diagram in
D
on the right), where
Y
2
=
(A,B)
and
Y
1
=
(A
×
B,A
×
B)
,
g
OP
=
(
k,l
,
k,l
)
:
(C,C)
→
(A
×
B,A
×
B)
, with
k
:
C
→
A,l
:
C
→
B
two arrows in
D
:
C
OP
(X,Y
1
)
C
OP
(X,Y
2
)
in this case
The bijective function
h
X
(f
OP
)
:
→
(A,B)
in
C
OP
(X,Y
2
)
(i.e., the
:
→
means that for any arrow
(k,l)
(C,C)
couple of arrows
k
:
C
→
A
,
l
:
C
→
B
in
D
) there is the unique arrow
B)
in
C
OP
(X,Y
1
)
(i.e., the unique arrow
:
→
×
×
(
k,l
,
k,l
)
(C,C)
(A
B,A
k,l
:
C
→
A
×
B
in
D
), such that the diagrams above commute.