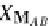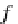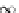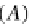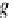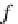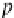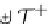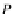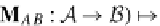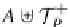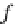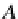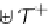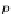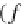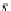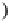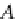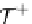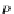Database Reference
In-Depth Information
where the inclusion
in
:
X
M
AB
→
X
represents the generation of new auxil-
iary variables in
X
from a given set of variables (defined by a mapping
M
AB
:
A
→
B
) during the process of flattening of the complex equations
α(r
q
i
)
=
q
i
∈
S
⊆
M
AB
Im(α(q
A,i
))
, for each
r
q
i
∈
X
M
AB
.
T
P
(T
∞
(A))
is defined, for any
The isomorphism (a bijection)
:
T
∞
(A)
→
A
ground-term tree
t
T
∞
(A)
, by:
•
(t)
=
t
∈
A
if
t
is a parameter;
t
∈
T
P
(T
∞
(A))
if
t
=
o
i
(t
1
,t
2
)
or
t
=
o
i
(t
1
)
,
while its inverse
∈
T
P
(T
−
1
:
A
(A))
→
T
(A)
, by:
∞
∞
∈
T
P
(T
•
−
1
(t)
(A))
.
Consequently, each pair
(α,
M
AB
)
which defines a morphism
f
=
t
if
t
∈
A
or
t
∞
α
∗
(
M
AB
)
=
:
A
→
T
P
)
-
coalgebra semantics represented by commutative diagram above, and hence the
coinduction is intimately linked with the morphisms in the
DB
category, dually to
the induction which is linked with the (closed) objects in the
DB
category.
Notice that the final coalgebra semantics, which defines the unique solution for
all variables in
r
q
i
X
M
AB
⊆
X
, will satisfy the schema mapping
M
AB
if each compo-
nent function
α(v
i
)
α
∗
(
B
)
in the
DB
category generates this coinductive process with final
(A
α
∗
(
:
f
s
(r
q
i
)
→
α(r
B
i
)
, where
α(r
B
i
)
∈
B
=
B
)
, of the morphism
α
∗
(
M
AB
)
α
∗
(
f
)
in the
DB
category, is an injection. In such a case, the
solution subset of relations in
=
:
A
→
B
defines the information
flux of this
DB
morphism
f
(as specified by the kernel of the information flux in
Definition
13
in Sect.
2.4.3
).
In Example
29
(Sect.
5.1.1
), we have remarked that the nullary operator (empty-
relation constant)
{
f
s
(r
q
i
)
|
r
q
i
∈
X
M
AB
⊆
X
}
Σ
R
can be used to build the relations. In fact, we may build a
tuple of a
k
-ary relation by the following set of equations with variables (relational
symbols) in
X
(we recall that
r
⊥∈
∅
∈
X
):
r
∅
≈⊥;
(it is always satisfied)
r
1
,
1
≈
EXTEND
r
∅
ADD
at(
1
), name
1
AS
name
1
=
d
11
;
r
1
,
2
≈
EXTEND
r
1
,
1
ADD
at(
1
), name
1
AS
name
1
=
d
12
;
···
r
1
,k
≈
EXTEND
r
1
,k
−
1
ADD
at(k), name
k
AS
name
k
=
d
1
k
,
so that
R
1
=
is a
k
-ary relation with this tuple. Anal-
ogously, we are able to construct all other
k
-ary tuples and hence, by using the
operation 'UNION', we obtain the final
k
-ary relation. Consequently,
every
relation
R
may be represented as a term of the
Σ
R
-algebra.
f
s
(r
1
,k
)
={
(d
1
k
,...,d
1
k
)
}