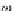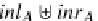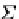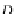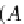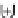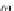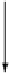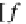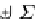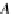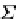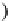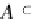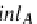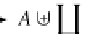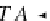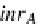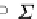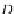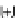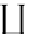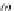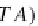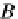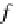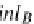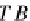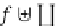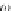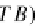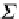Database Reference
In-Depth Information
Thus, we obtain the following corollary:
Corollary 32
For each simple object A in the
DB
category
,
there is the initial
ω
TA,
ω
TA) is a
Σ
A
-algebra
,
A
[
inl
A
, inr
A
]
,
where inl
A
:
A
→
(A
monomorphism
,
while inr
A
:
Σ
D
(A
ω
TA)
→
(A
ω
TA)is an isomorphism
.
This inductive principle can be used also to show that the endofunctor
T
:
(I
DB
ω
◦
DB
−→
DB
inductively extends to the composed endofunctor
E
=
T)
:
DB
→
DB
, where
I
DB
is the identity endofunctor for
DB
, while the endofunctor
ω
:
DB
is an
ω
-coproduct.
Indeed, to define its action
Tf
on an arrow
f
DB
→
:
A
−→
B
, take the inductive
ω
TB)
ω
TB)
(of the
(B
extension of
inr
B
:
Σ
D
(B
−→
(B
Σ
D
)
:
DB
−→
DB
endofunctor with initial
(B
Σ
D
)
-algebra structure
Σ
D
)
B
TB
B
TB
[
inl
B
, inr
B
]:
(B
−→
ω
ω
along the composite
inl
B
◦
f
, i.e.,
(inl
B
◦
f)
#
=
inl
B
◦
f, inr
B
◦
Σ
D
f
Tf
inr
O
A
=
f
◦
Tf.
ω
ω
The second diagram
ω
Tf)
commutes [
16
]. In fact, for the left square we have
(f
◦
inl
A
=
(f
ω
Tf)
id
A
,(
ω
Tf)
1
1
1
1
◦
⊥
=
◦
◦⊥
=
⊥
=
⊥
◦
=
id
A
,
f
f,
id
B
,
f
inl
B
◦
f
.
The proof that the right square commutes as well is the same as the proof given
above for the right square of the unique inductive extension of
h
D
along
f
.