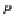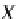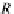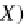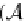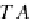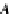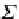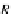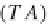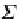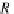Database Reference
In-Depth Information
8.3.1 DB Inductive Principle and DB Objects
We have shown in Sect.
5.1.1
that for any schema
A
and an R-algebra
α
which is
α
∗
(
a model of
)
is an object in
DB
, the set of views (relations)
TA
is determined from the
unique epic (X
A
, such that the simple instance-database
A
=
A
Σ
R
)
-
homomorphism
α
#
, from the initial
(X
Σ
R
)
-algebra
(
T
P
X,
)
into this
(X
Σ
R
)
-
algebra
(T A,
)
. This is represented by the commutative diagram in
Set
(here
X
is the set of relational symbols in database schema
[
α,h
A
]
A
)
where
Σ
R
and
T
P
X
are the SPRJU algebra and the set of its terms with variables in
X
, respectively, given by Definition
31
(see also Example
29
in Sect.
5.1.1
), with
}
i
X
X
2
}
.
X
ar(o
k
)
Σ
R
(X)
=
=
×{
i
×{
i
o
k
∈
Σ
R
o
i
∈
Σ
R
,ar(o
i
)
=
1
,i
≥
1
=−
1
,
0
Consequently, the
inductive principle
, used to construct unique
α
#
from
α
, is in strict
relationship with the properties of the
objects
in the
DB
category and especially with
the construction of closed objects that are
least fixed points
of the monotonic power-
view operator
T
. We will see that the dual
coinductive principle
is instead in a strict
relationship with the
morphisms
in the
DB
category.
From the fact that
DB
is an lfp category (Corollary
29
) enriched over the lfp sym-
metric monoidal closed category (Theorem
15
) with a tensor product
(matching
operator for databases), and the fact that
T
is a finitary enriched monad on
DB
(Theorem
16
), by Kelly-Power theorem,
DB
admits a presentation by operations
and equations, so that
DB
is the category of models [
17
] for an essentially algebraic
theory.
In what follows, we will use the category
DB
I
(the “poset” subcategory of
DB
with the same objects and with only monic arrows,
in
B
:
⊗
B
→
A
iff
B
A
(i.e.,
TB
TA
for the simple objects), introduced by Theorem
6
in Sect.
3.2.5
). Then
we will introduce a functor
Σ
D
:
⊆
DB
, where
DB
f
is a full subcategory
of
DB
I
composed of only
finite objects
(i.e., the databases), for the signature of
relational algebra w.r.t. the lfp category
DB
enriched over itself but where an arrow
is not a function (differently from standard algebra signature
Σ
R
defined over
Set
category where an arrow is a function) but
aset
of functions. This definition of
Σ
D
is
correct because all sigma operations
o
i
∈
DB
f
→
Σ
R
of a relational algebra are finitary, i.e.,
with arity
n
=
ar(o
i
)
being a finite number. Thus, a view-mapping arrow
f
o
i
:
A
→
TA
in
DB
, equal (from Definition
17
in Sect.
3.1.2
)to
α
∗
(
M
A
A
)
={
α(q
i
),q
⊥
}