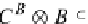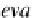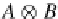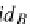Database Reference
In-Depth Information
f
ji
|
DB
(A
j
,B
i
)
A
B
f
ji
∈
1
≤
j
≤
m,
1
≤
i
≤
k
f
ij
|
DB
(B
i
,A
j
)
f
ij
=
f
OP
B
A
ji
∈
⊗
A
B,
1
≤
i
≤
k,
1
≤
j
≤
m
A
B
B
A
i.e.,
B
B
.
That is, the
cotensor B
A
(i.e., hom-object) of any two objects
A
and
B
, which is
a particular limit in
DB
, is equal to the corresponding colimit, that is,
tensor product
A
⊗
B
, of these two objects; this fact is based on the duality property of
DB
category.
⊗
A
A
⊗
8.2.1 DB Is a V-Category Enriched over Itself
Generally, a monoid
M
acting on the set
Ob
DB
may be seen as a general metric
space where for any
B
Ob
DB
the distance
C
B
S
(relations, or
views, in our case) whose action sends
B
to
C
(this action provides a possibility to
pass from the “state”
B
to “state”
C
of the database “system” of objects in
DB
), as
we investigated in the chapter dedicated to operational semantics for the database
mapping systems.
A monoidal category is closed if the functor _
∈
is a set of
R
∈
⊗
B
:
DB
−→
DB
has a right
adjoint
(
_
)
B
DB
for every object
B
,
((
_
)
B
,
_
:
DB
−→
⊗
B,η
⊗
,ε
⊗
)
:
DB
−→
DB
,
C
B
with the counit
ε
C
:
⊗
−→
B
C
called the evaluation at
C
(denoted by
eval
B,C
).
Theorem 15
,Υ) is a
monoidal bi-closed
:
for every object B
,
there exists in
Set
an isomorphism
(
abi-
jection
)
Λ
Strictly symmetric idempotent monoidal category (
DB
,
⊗
B,C)
=
DB
(A,C
B
) such that for any f
:
DB
(A
⊗
∈
DB
(A
⊗
B,C)
,
f
,
the hom-object C
B
together with a monomorphism eval
B,C
:
C
B
Λ(f )
≈
⊗
B
→
C
,
the following “exponent” diagram
commutes
,
with f
=
eval
B,C
◦
(Λ(f )
⊗
id
B
)
.
Proof
Let us consider the simple objects
A,B,C
and a morphism
f
=
α
∗
MakeOperads(
M
)
:
A
⊗
B
→
C,
:
A
α
B
→
C
α
∗
(
α
∗
(
obtained from a sketch's mapping
M
with
A
=
A
),B
=
B
)
and
. Thus.
f
⊆
T(A
⊗
B)
∩
TC
=
C
=
α
∗
(
C
)
obtained from the schemas
A
,
B
and
C
TA
∩
TB
∩
TC
.