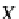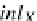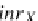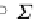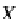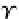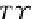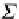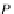Database Reference
In-Depth Information
well known that a relational database
scheme
can readily be viewed, with some
inessential abstraction involved, as a sketch. By Liar's theorem, a category
DB
is
accessible [
13
,
20
] because it is sketchable.
Remark
A standard application of sketches is used to define a theory of a
single
database scheme, so that objects of this graph-based logic theory are single rela-
tions of such a database and arrows between them are used to define the common
database functional dependencies, inclusion dependencies and other database con-
straints. Here, in the case of inter-database schema mappings, we need to use the
whole databases as objects in this lfp
DB
category: the price for this higher level of
abstraction is that arrows in
DB
are much more complex than in a standard setting,
and hence are not (simple) functions but the
sets of functions
.
Let us show that the top closed object
Υ
for the simple databases in
DB
,in-
troduced by Definition
26
, is a maximal database instance of a particular database
schema
Υ
, which defines the minimal cardinality for a set of relational symbols
(variables)
and its R-algebras
α
introduced for operads in Sect.
2.4.1
by Defini-
tion
10
(obtained as the extensions of Tarski's semantics of FOL).
R
Proposition 55
Let us define the minimal set of relational symbols by a bijection
α
0
:R→
Υ
,
so that the schema database for a closed object
Υ
in
DB
is equal to
Υ
α
0
(Υ)
.
Thus
,
for any other R-
=
(
R
,
∅
) and hence α
0
is an R-algebra with
Υ
=
α
0
,
α
∗
(Υ)
=
⊆
algebra α
Υ
,
so that the following initial Σ
R
-algebra semantics is
valid for
all
R-algebras α
That is
,
α
α
∗
(Υ)
=
{
}=
A
∈
Ob
DB
A
A
|
A is simple object in
DB
=
Υ
.
(
ω
Υ
)
.
The total object in
DB
is Υ
=
Υ
∪
Proof
From the bijection
α
0
:R→
Υ
, the minimal cardinality for the set of rela-
tional symbols
in our operads semantics for database mappings is determined by
the cardinality of the closed object
Υ
defined by Definition
26
.
So, for a defined schema
Υ
=
(
R
,
∅
)
and this R-algebra
α
0
,
α
0
(Υ)
R
=
α
0
(r)
∈
Υ
=
α
0
(r)
∈R
=
|
r
|
r
Υ
.
The
Σ
R
-algebra generated by the carrier set
Υ
,
Υ
Σ
=
(
Υ
,h
Υ
)
, is the bottom
horizontal arrow of the commutative diagram in
Set
above such that the func-
tion
h
Υ
, for each unary (or binary) operator
o
i
∈
Σ
P
=
Σ
R
and the relations
α
#
(t),α
#
(t
1
),α
#
(t
2
)
∈
T
Υ
=
Υ
, is defined by: