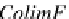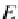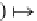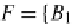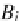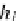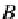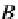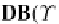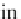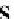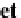Database Reference
In-Depth Information
deduce
C
⊗
A
C
⊗
B
, thus
|
DB
fin
(C,A)
|=|
DB
fin
(C,B)
|
, i.e., there is a bijection
υ
DB
fin
(C,B)
which is an isomorphism in
Set
. Thus,
DB
, which
is cocomplete and has this strong generator
DB
fin
,isanlfp.
:
DB
fin
(C,A)
→
Set
such that
DB
(A,B)
is
the hom-set of all morphisms in
DB
from
A
into
B
, and for any arrow
g
:
B
−→
C
,
DB
(A,g)
is the function such that for any morphism
f
∈
We define a representable functor
DB
(A,
_
)
:
DB
−→
DB
(A,B)
we obtain the
morphism
h
=
DB
(A,g)(f )
g
◦
f
∈
DB
(A,C)
.
Set
preserves colimits if the image
Hν
:
HF
−→
H ColimF
for the colimit
(ν, ColimF)
of a functor
F
∈
We say that a functor
H
:
DB
−→
DB
J
is a colim-
iting cone (or cocone) for
HF
. In this case, we are interested in
H
=
DB
(Υ,
_
)
.
Let us show, for example, that the object
Υ
is a finitely presentable (fp) (it was
demonstrated previously by remark that
Υ
=
{
=
TΥ
TA
|
A
⊆
ω
Υ
}
), i.e., the fact
that its hom-functor
DB
(Υ,
_
)
:
DB
−→
Set
preserves directed colimits:
Proposition 54
The total object
,
that is
,
the matching monoidal unit Υ is a finitely
presentable
(
fp
).
DB
J
,
where
F
can be seen as a base diagram for this
directed
colimit, composed of a fi-
nite number of (possibly complex) objects
B
1
,...,B
n
with PO-arrows “
∈
Proof
Let us consider the object
ColimF
in
DB
(a colimit of the functor
F
” between
them), such that the arrows
h
i
:
B
i
→
ColimF
are the monomorphisms correspond-
ing to partial ordering
B
i
ColimF
for directed colimits, as specified by Theorem
6
in Sect.
3.2.5
. These monomorphisms are the components of the cocone
(ν, ColimF)
where
ν
:
F
−→
ColimF
is a natural transformation (and
is a diagonal constant
functor) such that its components are
ν(B
i
)
n
. The translation
of this directed colimit diagram from
DB
into
Set
by using the functor
DB
(Υ,
_
)
,
for any cocone monomorphism
h
i
, can be represented by the following diagram:
=
ν
B
i
=
h
i
,
1
≤
i
≤
Thus, for this directed colimit and a set of all objects in the diagram (i.e., the
functor)
F
,
S
={
B
i
|
B
i
∈
F
}⊆
Ob
DB
,
ColimF
=
sup
(S)
=
sup
{
B
i
|
B
i
∈
F
}=
B
i
∈
F
B
i
=
B
i
∈
F
B
i
. Then for each monomorphism
h
i
:
B
i
ColimF
, from
h
i
Proposition
6
, any of its simple ptp arrows
h
ij
∈
is monic and hence with
h
ij
=
TB
i
.