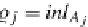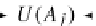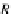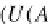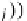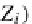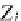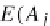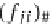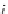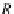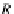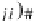Database Reference
In-Depth Information
=
1
≤
j
≤
m
U(A
j
)
and
(
1
≤
j
≤
m
j
)
where
U(A)
=
∈
E(A,U(A))
, i.e.,
:
1
≤
j
≤
m
A
j
−→
1
≤
j
≤
m
U(A
j
)
is an inclusion function and
U(A)
is a free alge-
bra over
A
(i.e., a quotient-term algebra generated by a carrier database instance
A
).
It is a disjoint union of the free algebras
U(A
j
)
over
A
j
,
j
=
1
,...,m
, such that
for any function
f
∈
E(A,Z)
,
f
:
A
→
Z
, with a set of point-to-point functions
=
1
≤
j
≤
k
Z
i
,k
f
f
ji
:
1, for each
f
ji
there
is a unique homomorphism
k
ji
from the free algebra
U(A
j
)
into an algebra
Z
i
, with
f
ji
=
A
j
→
Z
i
∈
for a complex object
Z
≥
◦
E(A
j
,k)
j
, represented by the following initial algebra semantics diagram
in
Set
:
The set of such unique point-to point homomorphisms
k
ji
:
(U(A
j
), inr
A
j
)
→
f
f
k
(Z
i
,h
i
)
, for each
f
ji
∈
={
k
ji
|
f
ji
∈
}
, that is, a unique
Σ
R
-algebra
homomorphism
k
:
(U(A), inr
A
)
→
(Z,h)
which corresponds to the unique homo-
morphism
k
from the initial
(A
define
Σ
R
)
-algebra
(U(A),
[
inl
A
, inr
A
]
)
into the algebra
(Z,
f
#
is a function equal to
k
but without the structural
properties of the homomorphism (to commute with operations of the algebra).
[
f,k
]
)
. Thus,
E(A,k)
=
Let us define now the faithful forgetful functor from
DB
into
Set
category:
(F
sk
,F
sk
)
Theorem 14
There exists a faithful forgetful functor F
sk
=
:
DB
sk
−→
Set
such that its object-component F
sk
,
while the arrow-component F
sk
,
for a given morphism f
:
A
→
B
,
where A
=
is equal to the powerset operator
P
1
≤
j
≤
m
A
j
,
m
=
1
≤
i
≤
k
B
i
,
k
≥
1,
and B
≥
1,
is defined as follows
:
for any set
S
∈
F
sk
(A)
=
P
(
1
≤
j
≤
m
A
j
)
,
F
sk
(f )(S)
⎧
⎨
f
}
∩
f
l
,(f
l
:
{
R
|
R
∈
S
A
→
B)
∈
if m
=
k
=
1
;
∈
f
j
1
,(f
j
1
:
f
{
R
|
(j,R)
∈
S and R
A
j
→
B
1
)
∈
)
}
if m
≥
2
,k
=
1
;
∩
f
1
i
,(f
1
i
:
f
⎩
{
|
∈
A
1
→
∈
}
=
≥
;
(i,R)
R
S
B
i
)
if m
1
,k
2
f
}
∈
f
ji
,(f
ji
:
{
(i,R)
|
(j,R)
∈
S,R
A
j
→
B
i
)
∈
otherwise.
We define the faithful forgetful functor F
DB
=
F
sk
◦
T
:
DB
−→
Set
as well
.
Consequently
,
DB
sk
and
DB
are concrete categories
.
Proof
The skeletal category
DB
sk
has the closed objects only, and hence for any
two closed objects (that are sets of relations)
A
=
TA
and
B
=
TB
, each
simple
arrow in
DB
between them
f
:
TA
−→
TB
(where
A
and
B
are simple databases)