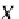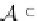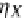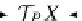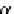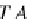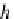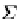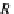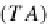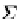Database Reference
In-Depth Information
Proof
Let us define
T
sk
=
T
1
, while
In
sk
and
In
sk
are two identity
functions. It is easy to verify that these two categories are equivalent. In fact, there
exists an adjunction
(T
sk
, In
sk
,η
sk
,ε
sk
)
T
0
and
T
sk
=
:
DB
−→
DB
sk
based on the bijection
σ
:
DB
sk
(T
sk
A,B)
→
DB
(A, In
sk
B)
which is natural in simple objects
A
∈
DB
and
∈
=
∈
B
DB
sk
(thus,
B
is closed, i.e.,
B
TB
). In fact, for each
f
DB
sk
(T
sk
A,B)
,
:
→
=
=
◦
is
A
:
whichisanarrow
f
TA
B
(from
T
sk
A
TA
), we define
σ(f)
f
→
∈
:
→
A
B
; conversely, for any
g
DB
(A, In
sk
B)
, which is an arrow
g
A
B
(from
is
−
1
A
is
−
A
=
B
), we define
σ
−
1
(g)
. Thus,
σ
−
1
(σ(f ))
=
=
◦
=
◦
◦
In
sk
B
g
σ(f)
f
is
−
A
=
is
−
A
)
is
−
A
◦
f
, and
σ(σ
−
1
(g))
is
A
◦
f
◦
id
TA
=
=
σ(g
◦
=
g
◦
is
A
=
g
◦
id
A
=
g
.
In a given inductive definition, one defines a value of a function on all (alge-
braic) constructors (i.e., relational operators), in our example the endofunctor
T
as explained in Sect.
5.1.1
, by the initial relational
(X
Σ
R
)
-algebra semantics
with the syntax monad
(
T
P
,η,μ)
. It is provided for a given assignment (R-algebra)
α
:
X
→
TA
, where
X
is a set of relational variables (symbols) in a database schema
α
∗
(
A
)
. This inductive definition is expressed by the following
commutative diagram in
Set
:
, such that
A
=
A
As we see, the
induction
for each schema
A
and R-algebra
α
, which is an interpre-
tation of
, defines the
closed objects
in
DB
.
The following is based on the fundamental results of the Universal algebra [
4
].
Based on Definition
31
of the Cod's SPRJU relational algebra,
Σ
R
is a finitary
signature (in the usual algebraic sense: a collection
Σ
R
of function
symbols
with
a function
A
giving the finite arity of each function symbol) for a
single-sorted (sort of relations) relational algebra. Here we will recall some Univer-
sal algebra concepts from Sect.
1.2
:
We can speak of
Σ
R
-equations
E
and their satisfaction in a
Σ
R
-algebra, obtain-
ing the notion of a
(Σ
R
,E)
-algebra theory. In a special case when
E
is empty, we
obtain a pure syntax version of Universal algebra, where
K
is a category of all
Σ
R
-
algebras and the quotient-term algebras are simply term algebras
ar
:
Σ
R
−→
N
T
P
X
for a given
set of relational variables
X
.
An
algebra
for the algebraic theory (or type)
(Σ
R
,E)
is given by a set
X
, called
the
carrier
of the algebra, together with interpretations for each of the function
symbols in
Σ
R
. A function symbol
o
i
∈
Σ
R
of arity
k
must be interpreted by a
X
k
function
o
i
:
−→
X
. Given this, a term containing
n
distinct variables gives
rise to a function
X
n
−→
X
defined by induction on the structure of the term. An