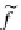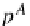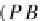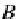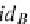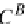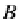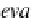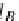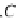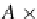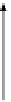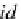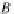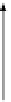Database Reference
In-Depth Information
Proof
For a morphism
f
we have that for each of its ptp arrows
f
ji
:
A
j
→
B
i
,
f
ji
⊆
TA
j
⊆
TB
i
. The first part comes directly from the proof of Proposition
48
in
the case when
C
=
B
and
g
=
id
B
, with
l
=
i
,
D
ilj
=
(T A
j
∩
g
ii
)
∪
(T A
j
\
f
ji
)
=
(T A
j
∩
TB
i
)
∪
(T A
j
\
f
ji
)
=
TA
j
A
j
and
(T B
i
∩
f
ji
)
=
f
ji
∪
=
f
ji
.
D
jli
=
∪
(T B
i
\
(T B
i
\
g
ii
)
TB
i
)
From the fact that
f
is a complex monomorphism, we have a ptp arrow for every
simple object
A
j
,1
≤
j
≤
M
, so from the commutativity we have that
Lim(f )
A
M
f
×
f
(we recall that the product '
A
1
···
A
×
' is equal to
). The rest
comes directly from it.
Remark
Consequently, for each morphism
f
:
A
→
B
such that for each of its ptp
arrows
f
ji
:
A
j
→
B
i
,
TA
j
⊆
TB
i
, the following commutative diagram with the
arrows
p
B
and
p
A
such that
p
B
τ
−
1
J(f)
and
p
A
id
A
=
=
is a pullback diagram:
If the category is finitely complete and has the
exponentiation
as well than it is a
Cartesian Closed Category (CCC). We say that a category has exponentiation if it
has a product for any two objects, and if for any given objects
B
and
C
there is an
object
C
B
and an arrow
eval
B,C
:
C
B
×
B
→
C
, called an
evolution
arrow, such that
C
B
for any object
A
and arrow
f
:
A
×
B
→
C
, there is a unique arrow
Λ(f )
:
A
→
making the following diagram commute:
such that
eval
B,C
◦
(Λ(f )
×
id
B
)
=
f
. The assignment of
Λ(f )
to
f
establishes a
B
to
C
and the arrows from
A
to
C
B
.
bijection
Λ
from the arrows from
A
×
It is well known that in a CCC with a zero object (i.e., when terminal and initial
objects are isomorphic) such a category degenerates, i.e.,
all
objects in such a cate-
gory are isomorphic. The
DB
category has a zero object
0
but does not degenerate:
⊥