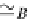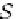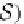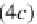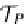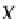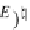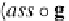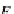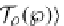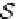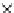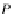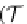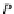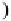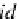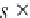Database Reference
In-Depth Information
Let us consider the following case when
m
=
℘
, i.e., when
m
:
X
→
B
P
X
repre-
[
]=
:
→
S
×
B
P
(X)
:
sents the behavior with
_
ass,℘
X
Proposition 42
Let us consider the commutative diagram
(8)
in the case when
m
=
℘
:
X
→
B
P
X represents the behavior
[
_
]=
ass,℘
of a program
.
Then
,
for
g
E
Z
,
the
commutative diagram
(4a)
in Sect
.
7.4
becomes the following commutative diagram
=
T
P
X
,
l
=
T
(℘) and an extended assignment f
=
ass
◦
:
T
P
X
→
S
g
E
)
where (ass
◦
:
T
P
X
→
D
P
S
is defined recursively by
:
@
1.
For any variable p
k
∈
X
⊆
T
P
X
,
p
k
→ [
p
k
]
∈
D
P
S
;
ass(
g
E
(nil))
0
,
a
ass(
g
E
(a))
,
for each a
→
=⊥
→
∈
2.
nil
Act
;
ass(
g
E
(a.t)) and
3.
a.t
→
L
∈
D
P
S
,
where fst(
L
)
=
=
ass
g
E
(t)
;
a
snd(
L
)
◦
n
(t
1
,...,t
n
)
g
E
)
(t
i
)
,
4.
→
L
∈
D
P
S
,
where
L
is the union of all trees (ass
◦
≤
≤
1
i
n
,
obtained by superposition of their roots in the unique root
ass
g
E
n
(t
1
,...,t
n
)
.
T
(℘)
for the variables
p
k
∈
Proof
Now it is enough to demonstrate the validity of
X
⊆
T
P
X
. In fact,
T
(℘)(p
k
)
=
℘(p
k
)
respects the behavior of the programs. The
g
E
and
recursive definitions of
ass
◦
T
(℘)
are the unique extensions of
ass
and
℘
from the variables to all terms in
T
P
X
, and hence the diagram (4c) is the unique
extension of the diagram (4) for the final
(
S
×
B
P
)
-coalgebra semantics to all terms
in
T
P
X
.
Due to the fact that in our database-mapping programs we start with processes
that are LTS systems, from the observational comonad
D
P
described in Sect.
7.4
,
we will present also the second (equivalent)
dual
approach to the SOS.
A Functorial Denotational Semantics for a syntax monad
T
P
and a behavior end-
ofunctor
B
P
is a
denotational comonad
D
ρ
which 'lifts' the observational comonad
(
D
P
,ε,δ)
(and inherits
ε
and
δ
from it) to the
Σ
P
-algebras of the syntactical monad
T
P
. We have seen that
Σ
P
and its coalgebraic dual
B
P
are two endofunctors on a co-
D
P
,ε,δ)
is the
cofree comonad generated
by
B
P
(dual to the algebraic syntax monad
D
P
=
cartesian category
Set
and that
(
T
P
=
(
T
P
,η,μ)
). It can be represented by
the following commutative diagram in
Cat
(we denote the category of
Σ
P
-algebras
by
Σ
P
-Alg
), where
U
Σ
P
denotes the forgetful functor: