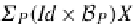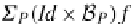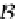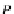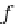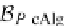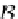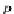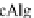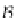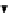Database Reference
In-Depth Information
=
(a
11
,p
k
1
1
),...,(a
n
1
1
,p
k
n
1
1
),...,(a
1
m
,p
k
1
m
),...,(a
n
m
m
,p
k
n
m
m
)
.
Notice that
p
i
and
p
i
1
,i
=
1
,...,m
(the root variables) are forgotten during ex-
ecution of these rules.
By using the universal property of coproducts
in
Set
, these functions can be
glued into a single function (application of rules)
Act
a
i
∈
×
B
P
X)
n
≥
X
:{
×
B
P
X)
n
nil
}∪
(X
(X
→
B
P
T
P
X,
Act
2
B
P
T
P
,
i.e., into
X
:
T
P
X)
with
:
Σ
P
(X
×
B
P
(X))
→
B
P
(
Σ
P
(Id
×
B
P
)
equal to that in [
39
].
Note one has a function
X
for each set
X
. Most importantly, the above definition
of
X
X
of variables in
X
(possibly
involving equating some of the variables), first renaming and then applying the rules
is the same as first applying the rules and then renaming, that is, the following
diagram commutes
is
natural
in
X
: for any renaming
f
:
X
→
B
P
T
P
and
Thus, we obtained the natural transformation
:
Σ
P
(Id
×
B
P
)
T
P
×
B
P
T
P
)
B
P
T
P
as in [
39
].
A Functorial Operational Semantics for a syntax monad
T
P
:
=
B
P
μ
◦
Σ
P
(
T
P
and a behavior
B
P
is the
operational monad
T
P
,η,μ)
(and in-
herits
η
and
μ
from it) to the coalgebras of the behavior endofunctor
T
which 'lifts' the syntactical monad
(
B
P
. It can be
represented by the following commutative diagram in
Cat
(we denote the category
of
B
P
-coalgebras by
B
P
-cAlg
), where
U
denotes the forgetful functor:
B
P
That is, every natural transformation
defines inductively a lifting (operational
monad)
T
of the monad
(
T
P
,η,μ)
to the
B
P
-coalgebras: given an operational