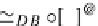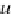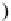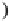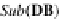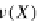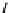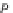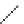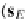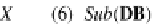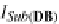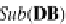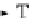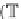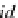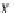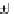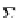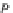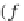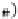Database Reference
In-Depth Information
If in this LTS we substitute any label '
a
' with the morphism '
f
a
' such that
f
a
=
Ta
, we obtain a diagram in
DB
category.
The subcategory
L
A
by inserting
the identity arrows for all vertices and all arrows that can be obtained from categorial
composition of
atomic
arrows (i.e., transitions in LTS
DB
(
L
A
)
is obtained from this graph (a tree)
L
A
).
Consequently, from Proposition
40
and the final coalgebra diagram (4), we ob-
tain the following final coalgebra diagram in
Set
, based on the
DB
category with
S
⊆
Ob
DB
:
@
In fact, for each
p
k
∈
X
, the trees
[
p
k
]
∈
D
P
S
=
gfp(
S
×
B
P
)
and
(
S
×
@
)
have the same traces (from the final coalgebra semantics diagram (4)),
B
P
)(
[[
p
k
]]
@
)
and
@
))
are two equivalent subcategories
so that
DB
(
[
p
k
]
DB
((
S
×
B
P
)(
[[
p
k
]]
[
p
k
]=
{
}
≥
=
of
DB
.Let
(A,
(a
1
,p
k
+
1
),...,(a
n
,p
k
+
n
)
)
, with
n
2 and
A
ass(p
k
)
.
Then the identity mapping
I
Sub(
DB
)
:
Sub(
DB
)
→
Sub(
DB
)
represents the mapping:
DB
[
@
→
DB
A,
a
1
,
@
,...,
a
n
,
@
,
p
k
]
[
p
k
+
1
]
[
p
k
+
n
]
@
by considering that the trees
L
A
=[
p
k
]
and
L
A
=
A,
a
1
,
@
,...,
a
n
,
@
[
p
k
+
1
]
[
p
k
+
n
]
are equal, but having only two different representations. Consequently, the diagram
above commutes.
Proposition 41
Sub(
DB
) in Propositions
39
and
40
,
the following commutative diagram represents the adequate DB-denotational
semantics for the operational semantics based on the
DB
category
:
From the bijection
DB
:
D
P
S
→