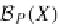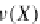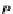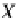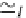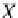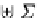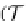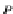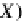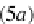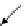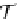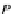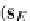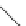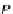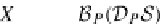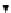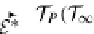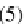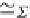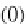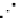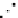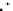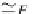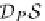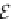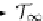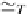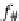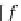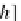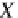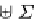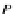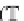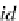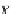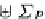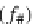Database Reference
In-Depth Information
E
∗
=
T
P
(
E
)
◦
ν(
D
P
S
)
,
f
=
T
◦
where
s
E
and
B
P
=
S
×
B
P
.
Proof
The commutativity of the diagram (4) is demonstrated in Sect.
7.4.2
;the
commutativity of (0) is proved in Proposition
37
for the final semantics of the system
of flattened equations
E
specified by
g
E
:
→
T
P
X
or, dually, by
g
E
X
:
T
P
X
→
X
(in Proposition
34
) and its solution
s
E
:
→T
∞
.
Let us demonstrate the commutativity of the diagram (5) (the embedding of the
LTS trees in
X
D
P
S
into the ground tree-terms in
T
∞
). We have the following cases:
E
∗
(A,
1. A single-node tree
A
∈
D
P
S
. Then
B
(A)
=
(A,
∅
)
and
∅
)
=
T
P
(
E
)
◦
ν(
D
P
S
)(A,
∅
)
=
T
P
(
E
)(A)
=
E
(A)
=
A
. While,
Σ
◦
E
(A)
=
Σ
(A)
=
A
.
Σ
◦
E
(A)
=
E
∗
◦
B
(A)
.
2. A tree
Thus,
L
A
∈
D
P
S
with a unique branch
a
from its root
A
. Then
B
(
L
A
)
=
E
∗
(A,
(A,
{
(a,
L
B
)
}
)
and
{
(a,
L
B
)
}
)
=
T
P
(
E
)
◦
ν(
D
P
S
)(A,
{
(a,
L
B
)
}
)
=
T
P
(
E
)(a.
L
B
)
=
a.
E
(
L
B
)
. While,
Σ
◦
E
(
L
A
)
=
Σ
(a.
E
(
L
B
))
=
a.
E
(
L
B
)
.
Σ
◦
E
(
L
A
)
=
E
∗
◦
B
(
L
A
)
.
3. A tree
Thus,
L
A
∈
D
P
S
with
n
≥
2 branches from its root
A
. Then
B
(
L
A
)
=
(A,
{
(a
1
,
L
B
1
),...,(a
n
,
L
B
n
)
}
)
and
E
∗
A,
(a
1
,
L
B
n
)
L
B
1
),...,(a
n
,
)
A,
(a
1
,
L
B
n
)
=
T
P
(
E
)
◦
ν(
D
P
S
L
B
1
),...,(a
n
,
)
L
B
n
}
=
n
a
1
.
L
B
n
)
.
n
=
T
P
(
E
{
a
1
.
L
B
1
,...,a
n
.
E
(
L
B
1
),...,a
n
.
E
(
At the same time,
=
Σ
n
a
1
.
L
B
n
)
Σ
◦
E
(
L
A
)
E
(
L
B
1
),...,a
n
.
E
(
n
a
1
.
L
B
n
)
.
=
E
(
L
B
1
),...,a
n
.
E
(
=
E
∗
◦
B
(
Consequently,
Σ
◦
E
(
L
A
)
L
A
)
.
From the fact that both
g
E
and
are based on the sets
S
(A,α
∗
)
(in Definition
54
)
for the outgoing arrows in
G
from a schema database
[
_
]
A
, it is easy to verify that
g
E
=
ν(X)
◦[
_
]:
X
→
T
P
(X)
. In fact, based on the algorithm
DBprog
, for each
p
k
∈
X
we have one of the following two cases: