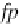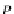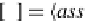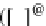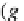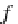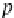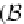Database Reference
In-Depth Information
The fact that the nodes have no names reflects the
abstractness
of these global
behaviors. Consequently, we are free to assign the names to nodes, and we will use
a name
p
k
(for this state
ass(p
k
)
∈
S
A
, an instance of a schema
) for a node name
instead of the 'process
p
k
at state
ass(p
k
)
'.
Consequently, for any DB-mapping system represented by a given graph
G
(a
program) with the set of the processes
p
k
in the states
ass(p
k
)
∈
S
∈
S
(i.e., in different
instance-databases
ass(p
k
)
for the database schemas in
G
), a single total meaning
function is given in Proposition
34
by
×
X)
.It
defines a one-to-on
e c
orrespondence between the transition systems and co-algebras
of the endofunctor
[
_
]=
ass,℘
:
S
−→
S
×
P
fin
(Act
B
P
=
S
×
B
P
=
S
×
P
fin
(Act
×
_
)
:
Set
−→
Set
, so that the di-
agram bellow commutes.
Final
(
S
×
B
P
)
-coalgebra diagram in
Set
(
B
is an isomorphism-bijection)
The coalgebras of the Power-set functor
P
are the same as the directed 'locally-
small' graphs (the tree
L
A
is a pointed (by
A
) accessible graph) and, by anti-
foundation axiom (
V
=
P
(V )
, for the universe
V
of all (also non-well-founded)
sets, is a final
-algebra), the
final coalgebra
is the class of rooted 'locally small'
trees (possibly of infinite depth) factored by
P
-bisimulation. A (possibly large)
graph is
locally small
if the (possibly infinite) collection of children of every node
is a (small) set.
The coalgebras are suitable to modeling the operational behavior of the programs
of a language. The corresponding endofunctors
P
B
P
are called
behavior endofunc-
tors
.
The final
(
S
×
B
P
)
-coalgebra
(gfp(
S
×
B
P
),
B
)
, where
gfp(
S
×
B
P
)
=
S
×
B
P
(gfp(
S
×
B
P
))
, is the greatest fixpoint of the behavior endofunctor, i.e., the set of
rooted 'locally-small' (finitely branching) trees (of possibly infinite depth) factored
by a strong bisimulation: for any database
A
, a labeled tree
L
A
with nodes in
S
and
branches in
Act
is an element of the set
D
P
S
=
gfp(
S
×
B
P
)
, obtained by the union
of the chain (here
1
is a singleton
P
fin
(
∅
)
={∅}
, that is, terminal object in
Set
)
∅⊆
S
×
B
P
(
∅
)
=
S
×
P
fin
(
∅
)
⊆
S
×
B
P
S
×
B
P
(
)
⊆···
=
S
×
1
S
⊆
S
×
B
P
(
S
)
S
,
i.e., obtained by iterating the functor
S
×
B
P
on the empty set of states
∅
,uptothe
greatest fixed point (with
S
⊆
D
P
S
, so that for each single-node tree
A
∈
S
⊆
D
P
S
,
B
(A)
=
∅
∈
S
×
B
P
(
D
P
S
(A,
)
)
).