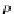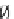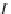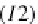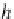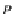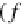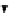Database Reference
In-Depth Information
Thus, for any other
(X
Σ
P
)
-algebra,
l
=[
f,h
]:
X
Σ
P
(Z)
−→
Z
(where
f
:
X
→
Z
and
h
:
Σ
P
(Z)
→
Z
, there is a unique arrow
f
#
to it from this initial
(X
Σ
P
)
-algebra such that
l
◦
(X
Σ
P
)(f
#
)
=
f
#
◦[
inl
X
, inr
X
]
, where
n
f
#
,i
n
≥
Σ
P
(f
#
)
=
id
Act
∪{
nil
}
f
#
×···×
f
#
a
i
∈
Act
2
with
f
#
,i
:
T
P
X
×{
i
}→
Z
×{
i
}
for each action
a
i
∈
Act
such that
f
#
,i
(t,i)
=
(f
#
(t),i)
, and
f
#
×···×
(f
#
(t
1
),...,f
#
(t
n
))
such that the left dia-
gram in
Set
bellow commutes (note that the diagram (I1) corresponds to the unique
homomorphism
f
#
:
f
#
(t
1
,...,t
n
)
=
(
T
P
X,
I
)
→
(Z,l)
, from the initial “syntax”
(X
Σ
P
)
-
algebra to another
(X
Σ
P
)
-algebra)):
If the set of variables
X
is the empty set
∅
(thus
f
is the empty function, with empty
graph), with
S
in
Set
, we obtain the simpler commutative diagram above on
the right, where the unique homomorphism
f
#
:
T
P
∅→
Z
represents the
meaning
of the ground terms in
∅
S
. Note that the right commutative diagram (I2) repre-
sents the unique homomorphisms
f
#
from the initial
Σ
P
-algebra of
ground terms
(
T
P
∅
,
I
∅
)
where
T
P
∅
I
∅
is an isomorphism equal to into
inr
X
for
X
=∅
, into the
Σ
P
-algebra
(Z,h)
.
We can see in which way the mapping
f
#
:
T
P
X
→
Z
is the unique induc-
tive extension of the assignment
f
:
X
→
Z
(such that for any variable
p
k
∈
X
,
=
T
P
X
, by these examples:
f
#
(p
k
)
f(p
k
)
) to all terms with variables in
∈
1. Let
(p
k
)
X
be a free variable in
X
and hence from the left commutative dia-
gram above
f
#
(
I
(p
k
))
=
f
#
(p
k
)
=
f(id
X
(p
k
))
=
f(p
k
)
. Thus, the reduction
⊆
T
P
X
is equal to the function
f
.
2. Let
(p
k
,
4
)
of
f
#
to
X
∈
X
×{
4
}
. Then,
I
(p
k
,
4
)
=
a
4
.p
k
∈
T
P
X
, and from the commu-
tativity
f
#
(
I
(p
k
,
4
))
=
f
#
(a
4
.p
k
)
=
h(f
#
,
4
(p
k
,
4
))
=
h(f
#
(p
k
),
4
)
=
h(f (p
k
),
4
)
=
(
when
Z
is a DB-denotational semantics, see bellow
)
=
a
4
⊗
f(p
k
)
.
∈
T
P
X
2
. Then,
3. Let
(a
4
.p
k
,t
2
)
I
(a
4
.p
k
,t
2
)
=
a
4
.p
k
t
2
∈
T
P
X
, and from
the commutativity we have that
f
#
(
I
(a
4
.p
k
,t
2
))
=
f
#
(a
4
.p
k
t
2
)
=
h((f
#
×
f
#
)(a
4
.p
k
,t
2
))
=
h(f
#
(a
4
.p
k
),f
#
(t
2
))
=
(
when
Z
is a DB-denotational
f
#
(t
2
)
.
The inductive principle can be used to show that the operator
semantics
)
=
(a
4
⊗
f(p
k
))
+
T
P
inductively extends
to the
syntax
endofunctor (in Sect.
5.1.1
)
T
P
:
Set
→
Set
(the
syntax
monad freely
generated by signature
Σ
P
).