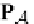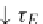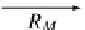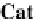Database Reference
In-Depth Information
2. For
j
≤
n
,
λIn
∗
ER
Out
U
st(i)
=
i
≤
j
+
λIn
∗
ER
Out
U
st(j)
=
λIn
∗
ER
(n,
0
,L)
=
id,
so that
F
P
st(i)
=
λIn
∗
ER
(Out
U
st(i)
κ
st(i)
λIn
∗
ER
Out
U
st(j)
st
(k)
=
st
(k
=
+
1
).
i
,
λIn
∗
ER
(Out
U
(st(i)))
λIn
∗
ER
(
id
and hence
F
P
(st(i))
3. For
j
+
n
+
1
≤
=
{}
)
=
=
st
(m)
.
Let us define a sequential composition of two programs
P
1
and
P
2
by
P
id(κ(st(i)))
=
κ(st(i))
=
P
1
where
N
is the biggest value of the address of instructions in the program
P
1
. Then
we define a program
P
+
N
2
=
P
2
◦
obtained by augmentation of each address in the instruc-
P
+
2
is the sequential concatenation
such that after the execution of
P
1
the machine will continue the execution of
P
2
.
Consequently, we are able to define a category with the sequential composition
of programs with SQL statements over a given database schema:
tions of
P
2
by
N
+
1. Consequently,
P
=
P
1
∪
A
Definition 41
where the
objects are the sequential compositions of the source programs with SQL statements
over this schema
Let
be a database schema. We define a category
P
A
A
, while the arrows are the actions
P
◦
_
:
P
1
→
P
2
such that
P
2
=
P
◦
P
1
is the program obtained by sequential composition of
P
1
and
P
.
_ where
P
NOP
is the program com-
posed of only one instruction NOP. The associativity of composition of the arrows is
guaranteed by the associativity of the sequential composition of the programs, thus
P
Each identity arrow in
P
is equal to
P
NOP
◦
A
is well defined.
A
Corollary 20
For every database schema
A
there are the following functors
:
Ob
P
A
,
U
M
(P )
=
1.
U
M
:
U
P
is the
category obtained from ATrS
U
(
by Proposition
29
),
and for an arrow P
◦
P
A
→
Cat
such that for each program P
∈
_
:
U
M
(P
P
1
→
P
2
we obtain an inclusion functor in
=
◦
_)
:
U
P
1
→
U
P
2
.
Ob
P
A
,
R
0
M
(P )
=
2.
R
M
:
R
P
is the
category obtained from ATrS
R
(
by Proposition
29
),
and for an arrow P
◦
P
A
→
Cat
such that for each program P
∈
_
:
=
R
1
M
(P
◦
P
1
→
P
2
we obtain an inclusion functor in
_)
:
R
P
1
→
R
P
2
.
Consequently
,
there
is
an
“embedding”
natural
transformation τ
E
:
R
M
,
U
M
such that for any program P
,
we obtain the functor
(
an arrow in
Cat
)
τ
E
(P )
=
F
P
:
U
P
→
R
P
(
defined in point
3
of Proposition
29
).