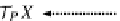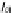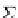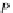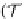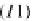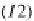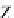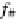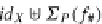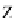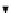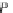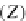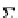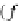Database Reference
In-Depth Information
postulating that “the universe
P
S
-algebra.” This provides
the formal link between the initiality and a (generalized) induction on well-founded
relations.
For the signature endofunctor
Σ
P
and every set of program variables
X
,the
initial
Σ
P
-algebra (Lambek's Lemma) are isomorphisms (for the carrier set
P
S
(V )
=
V
is an initial
T
P
X
),
(X
Σ
P
)(
T
P
X)
I
T
P
X
with the isomorphism (bijection in
Set
),
I
=[
inl
X
, inr
X
]:
X
Σ
P
(
T
P
X)
−→
T
P
X
, where
inl
X
:
−→
T
P
X
are injective arrows
of the coproduct
X
Σ
P
(
T
P
X)
. Consequently, the
(
T
P
X,
[
X
→
T
P
X
and
inr
X
:
Σ
P
(
T
P
X)
inl
X
, inr
X
]
)
is the initial
[
]
(X
Σ
P
)
-algebra and, consequently, for any other
(X
Σ
P
)
-algebra
(Z,
h,f
)
algebra (for each constant
o
i
,
ar(o
i
)
=
0 and
h(o
i
)
=
o
i
∈
Z
)thereisa
unique
homomorphism
f
#
:
(
T
P
X,
[
inl
X
, inr
X
]
)
→
(Z,
[
h,f
]
)
, as represented in the fol-
lowing commutative diagrams:
The left commutative diagram (I1) in
Set
corresponds to the unique homomorphism
f
#
:
(
T
P
X,
I
)
→
(Z,l)
, from the initial “syntax”
(X
Σ
P
)
-algebra to another
(X
Σ
P
)
-algebra)). If the set of variables
X
is the empty set
∅
(and hence
f
is the
empty function, with empty graph) with
S
in
Set
, we obtain the simpler
commutative diagram above (I2) on the right (note that in
Set
the object
∅
S
∅
S
is
isomorphic to
S
for any set
S
), where the unique homomorphism
f
#
:
T
P
∅→
Z
represents the
meaning
of the ground terms in
. Note that the right commutative
diagram (I2) represents the unique homomorphisms
f
#
from the initial
Σ
P
-algebra
of
ground terms (
T
P
∅
T
P
∅
,
I
∅
)
where
I
∅
is an isomorphism equal to into
inr
X
for
X
, into the
Σ
P
-algebra
(Z,h)
.
This commutative diagram for the initial algebra with variables in
X
can be rep-
resented in the following way as well: by inductive extension (principle), for every
Σ
P
-algebra structure
h
:
Σ
P
Z
−→
Z
and every mapping
f
:
X
−→
Z
, there is the
unique (inductive extension of
h
along the mapping
f
) arrow
f
#
:
T
P
X
=∅
Z
such
that the following first diagram (in
Set
) commutes (the first diagram bellow is just
recombination of the commutative diagram (I1). The second diagram is a particular
case of the first diagram, where
Z
is replaced by
−→
T
P
Z
and the mapping
f
:
X
→
Z
by the mapping
inl
Z
◦
f
:
X
→
T
P
Z
):