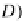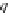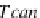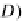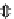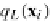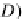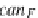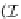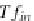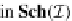Database Reference
In-Depth Information
In fact, from the fact that
h
q
=
h
q
F
=
=
f
in
=
Flux(α,
M
)
⊆
T can
F
(
I
,D)
GG
Tf
in
=
T f
in
, we obtain
Tf
in
∩
h
q
F
=
h
q
∩
f
in
and hence
Tf
in
◦
h
q
F
=
h
q
◦
f
in
.
In fact, we introduced marked null values (instead of Skolem functions) in order
to define and materialize such a
finite
database
can
F
(
I
,D)
.It
is not
a model of
the data integration system (which is infinite); however, it has all necessary query-
answering properties: it is able to provide all certain answers to conjunctive queries
over a global schema. Consequently, it can be materialized and used for query an-
swering, instead of methods based on the query-rewriting algorithms.
The procedure for computation of a finite canonical database for the global
schema, based on “immediate consequence” monotonic operator
T
B
defined in
precedence, can be intuitively described as follows: it starts with an instance
∅
which consists of
I
, instance of the source schema, and of the empty instance
G
I,G
∅
for the target (global schema) such that
R
={}
(i.e., empty relation with only an
0
empty tuple
) for each relation in
G
∅
(we recall that
G
∅
⊥
in
DB
). Then we
chase
(a finite set of source-to-target
dependencies) and
Σ
G
(a finite set of target (global schema) integrity dependencies)
as long as they are applicable. This process may fail (if an attempt to identify two
domain constants is made in order to define a homomorphism between two con-
secutive target instances) or it may never terminate. Let us denote two consecutive
target instances of this process (with
J
0
=
G
∅
I,G
∅
by applying all the dependencies in
M
)by
J
i
and
J
i
+
1
. Then we introduce
this “chase” function
C
h
:
Θ
−→
Θ
where
Θ
is the set of all pairs
I,J
,
I
is a
source instance and
J
one of target instances generated by
I
such that
C
h
I,J
i
.
I,J
i
+
1
=
Let us define the partial ordering
over the set
Θ
w
={
J
i
|
I,J
i
∈
Θ
}
such that
J
i
J
k
iff
∀
r
∈
J
i
(T
w
{
r,
⊥}⊆
T
w
{
σ(r),
⊥}
)
, where
σ
:
J
i
→
J
k
is a bijection such
that for each
r
∈
J
i
,
r
⊆
σ(r)
.
:
Θ
w
−→
Proposition 19
There exists the monotonic function Ψ
Θ
w
such that its
least fixpoint is obtained from J
0
=
G
∅
in a finite number n
≥
1
of steps and is equal
to can
F
(
I
,
D
)
=
Ψ
n
(J
0
)
.
Proof
We can define the function
Ψ
:
Θ
w
−→
Θ
w
such that for each
J
i
∈
Θ
w
:
Ψ(J
i
)
=
J
i
+
1
if
J
i
+
1
J
i
is not true;
J
i
otherwise.