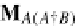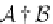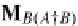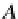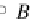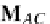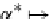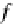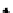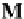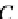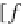Database Reference
In-Depth Information
sketches
, which are fundamentally small categories obtained from graphs enriched
with concepts such as (co)cones mapped by functors in (co)limits of the base cat-
egory
Set
. It was demonstrated that, for every sentence in basic logic, there is a
sketch with the same category of models and vice versa [
14
]. Accordingly, sketches
are called graph-based logic and provide very clear and intuitive specification of
computational data and activities. For any small sketch
E
, the category of models
Mod(
E
)
is an accessible category by Lair's theorem and reflexive subcategory of
Set
E
by Ehresmann-Kennison theorem. A generalization to base categories other
than
Set
was proved by Freyd and Kelly in 1972 [
5
].
In what follows, we substitute the base category
Set
by this new database cate-
gory
DB
. In fact, we translate each database mapping logic theory based on SOtgds
into an algebraic theory expressed by a sketch-category
Sch
(G)
where all arrows
are R-algebra terms. Then we describe R-algebraic structures using these sketch-
categories for theories and
α
functors into base category
DB
in order to obtain the
models of the database-mapping theories.
For instance, the
sketch
category
Sch
(G)
for the separation-composition map-
ping cocone diagram (graph
G
), introduced in Sect.
3.1
, is presented on the left-hand
side commutative diagram below. Notice that the mapping arrow
M
in a graph
G
is
replaced by the morphism
M
)
in this sketch, while the nodes
(objects) are eventually augmented by introducing another auxiliary schema
=
MakeOperads(
M
A
as
explained in Proposition
16
. The functorial translation (with a R-algebra
α
∗
)ofthis
sketch into the
DB
category has to be a coproduct diagram in
DB
(see Definition
27
and Theorem
5
):
α
∗
(
M
)
α
∗
(
M
aC
),α
∗
(
M
BC
)
where
M
=[
M
AC
,
M
BC
]
,
k
=
=[
]=[
f,g
]
, with the
α
∗
(
M
A(A
†
B)
)
and
in
B
=
α
∗
(
M
B(A
†
B)
)
, and the instance-
monomorphisms
in
A
=
α
∗
(
α
∗
(
α
∗
(
=
A
=
B
=
C
databases
A
)
.
As we explained in the introduction to sketch data models (Sect.
3.1.1
),
in a database mapping system expressed by a graph
G
, we never use the
“commutative diagrams” as the left diagram above (but only the arrow
M
),B
)
and
C
=
[
M
AC
,
M
BC
]:
A
†
B
→
C
or, more frequently, two simple arrows
M
AC
=
γ(
M
AC
)
=
MakeOperads(
M
AC
)
:
A
→
C
and
M
BC
=
γ(
M
BC
)
=
MakeOperads(
M
BC
)
:
B
→
C
Sch
(G)
is a simple small
category, i.e., 4-tuple
(G,u,D,C)
where
D
and
C
are empty sets. Consequently,
these database-mapping sketches are more simple than the sketches used for defini-
tion of Entity-Relationship models of single relational databases.
) and hence our sketch
E
=