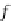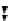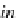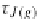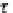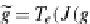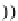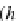Database Reference
In-Depth Information
2-cells “inclusions”) and also all higher
n
-cells [
2
], with their direct representation
by 1-cell morphisms.
Example 24
Let us consider the two ordinary simple morphisms (1-cells) in
DB
,
D
such that
f
f
TD
.We
want to show that the 1-cell corresponding monomorphism
β
:
f
→
g
is a result of
the symmetric closure functor
T
e
. We define two arrows
h
1
=
:
A
−→
B
and
g
:
C
−→
⊆
g
(thus,
f
g
) and
g
⊆
TC
∩
is
−
C
◦
in
C
◦
τ(J(f))
is
−
D
◦
(τ
−
1
J(f)
)
OP
(where
in
C
:
f
and
h
2
=
in
D
◦
→
TC
is a monomorphism, well
defined in Proposition
7
because
f
TC
,
is
−
C
:
⊆
g
⊆
TC
−→
C
is an isomor-
phism,
in
D
:
f
TD
is a monomorphism from Proposition
7
and
f
→
⊆
g
⊆
TD
,
D
is an isomorphism). Hence,
h
1
=
is
−
C
∩
in
C
∩
τ(J(f))
and
is
−
D
:
TD
−→
=
T f
∩
f
=
f
(because
TC
⊇
f
and
T f
=
f
) and, analogously,
h
2
=
TC
∩
⊇
g
is
−
D
∩
in
D
∩
(τ
−
1
T f
∩
f
=
f
(because
TD
⊇
f
and
T f
=
f
).
J(f)
)
OP
=
TD
∩
⊇
g
Thus,
g
h
1
=
h
2
◦
=
f
and hence
g
f
.
Thus, there exists the arrow
β
=
T
e
(h
1
;
h
2
)
:
J(f)
−→
J(g)
in
DB
◦
f
◦
h
1
=
h
2
◦
↓
DB
, and
the following commutative diagram in
DB
:
f
Let us show that also
T
e
(h
1
;
h
2
)
is a monomorphism with
β
=
T
e
(h
1
;
h
2
)
→
g
.
In fact,
h
2
=
f
and, by definition in Theorem
4
,
T
e
(h
1
;
in
OP
h
2
)
g
◦
T(h
2
◦
f)
◦
in
f
.
=
in
OP
g
∩
Th
2
∩
Tf
∩
f
=
f
and, consequently,
Thus,
T
e
(h
1
;
h
2
)
∩
in
f
=
g
T
e
(h
1
;
h
2
)
is a monomorphism (from Corollary
9
). In the particular case of The-
orem
6
when
A
D
and
is
−
C
◦
τ
OP
f
OP
ep
and
is
−
D
◦
=
C
and
B
=
in
C
=
J(f)
=
in
D
=
f
in
, we obtain that the 2-cell's arrow
√
β
f
−→
τ
−
1
J(f)
=
:
g
is represented by the
T
e
(f
OP
f
OP
in
:
f
1-cell monomorphism
β
=
ep
◦
f
ep
;
f
in
◦
)
→
g
.
Let us define the full subcategory of
DB
composed of only simple objects: