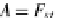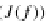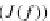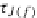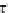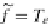Database Reference
In-Depth Information
τ
J(f
ji
)
:
,
τ
J(f)
=
f
A
j
f
ji
|
(f
ji
:
A
j
→
B
i
)
∈
and
τ
−
1
.
τ
−
1
J(f)
=
f
J(f
ji
)
:
f
ji
→
B
i
|
(f
ji
:
A
j
→
B
i
)
∈
In fact, from Proposition
3
in Sect.
2.5
, for a simple morphism
f
=
α
∗
MakeOperads(
M
AB
)
:
A
→
B,
α
∗
(
M
E
)
α
∗
(
M
M
)
we have two instance-mappings
ep(f )
=
:
A
→
TC
and
in(f )
=
:
C
=
(S
C
,
∅
)
,
S
C
=
q
i
∈
M
E
∂
1
(q
i
)
={
r
q
1
,...,r
q
m
}
and
C
=
α
∗
(S
C
)
.
TC
→
B
with
⊆
f
, we can define the equivalent morphisms
to these two morphisms, by substituting the instance-database
TC
by
f
and
hence defining the epimorphism
τ
J(f)
Tα
∗
(S
C
)
=
From the fact that
TC
α
∗
(
M
E
)
f
(from Proposition
3
,
:
A
τ
J(f)
=
ep(f )
=
f
) and the monomorphism
τ
−
1
:
f
α
∗
(
M
M
)
J(f)
→
B
(from
Proposition
3
,
τ
−
1
=
f
).
Notice that the existence of this monomorphism is also predicted by Propo-
sition
7
with monic “inclusion”
f
TB
(i.e.,
in
B
:
f
→
TB
and isomorphism
is
−
B
:
J(f)
=
in(f )
B
which is monic as well and hence their composition is a monomor-
phism equal to
τ
−
1
TB
is
−
B
◦
in
B
:
f
B
. In the same way, from Proposition
3
,
from the epimorphism
in
O
A
:
TA
f
(the dual (inverted) of the monomorphism
in
A
:
f
J(f)
=
→
TA
which is epic as well, we obtain
that their composition is epic as well. That is,
τ
J(f)
=
→
TA
) and isomorphism
is
A
:
A
in
O
A
◦
f
is an
is
A
:
A
epimorphism.
Remark
For any given morphism
f
:
A
f
is an epimorphism, and the arrow
f
in
=
τ
−
1
(J(f ))
:
f
→
B
is a monomor-
phism, so that
any
morphism
f
in
DB
is a composition of
an epimorphism and
monomorphism f
:
A
−→
B
in
DB
, the arrow
f
ep
=
τ(J(f))
=
f
in
◦
f
ep
(as in
Set
, in Example
1
), with the intermediate object
equal to its information flux
f
.
The particular cases with
-composed complex objects and complex arrows be-
tween them will be presented in more detail also in point 4 of Corollary
12
in
Sect.
3.3.2
.