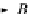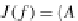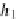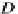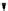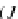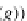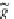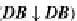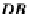Database Reference
In-Depth Information
f
∈
f
ji
}:
=
{
id
R
|
R
TB
i
→
TA
j
|
(f
ji
:
A
j
→
B
i
)
∈
(
from Theorem
3
)
Tf
OP
Tf
OP
f
=
ji
:
TB
i
→
TA
j
|
(f
ji
:
A
j
→
B
i
)
∈
=
.
in
OP
Tf
OP
Consequently, from Definition
23
, we obtain
in
f
OP
◦
f
=
:
TB
→
TA
.
Now we are ready to demonstrate that the
DB
category is a conceptually closed
extended symmetric category, w.r.t. Definition
5
in Sect.
1.5.1
, with introductions
of the encapsulation operator
J
such that for each morphisms
f
:
A
→
B
in
DB
,
J(f)
=
A,B,f
is an object in the arrow (or comma) category
DB
↓
DB
with its
inverse operator
ψ
such that
ψ(J(f))
=
f
.
Theorem 4
The category
DB
is an extended symmetric category
,
closed by the
(T
e
,T
e
)
DB
,
where T
e
=
functor T
e
=
:
(
DB
↓
DB
)
−→
B
T
ψ is the object com-
B in
DB
,
T
e
(J(f ))
=
f
,
ponent of this functor such that for any arrow f
:
A
→
while its arrow component T
e
is defined as follows
:
Fo r a n y a r row (h
1
;
h
2
)
:
J(f)
−→
J(g) in
DB
↓
DB
(
so that g
◦
h
1
=
h
2
◦
f
f
OP
:
f
→
TAand in
in
DB
),
T
e
(h
1
;
h
2
)
in
OP
g
◦
T(h
2
◦
f)
◦
in
f
OP
,
where in
:
g
g
→
TDare two monomorphisms
(
Proposition
7
).
This is represented by
The associative composition operator for objects
∗
,
defined for any fitted pair g
◦
f
of arrows
,
satisfies B
T
(g)
∗
B
T
(f )
g
◦
f
=
B
T
(g
◦
f)
.
α
∗
(
M
AB
)
Proof
Let us consider a simple morphism
f
=
:
A
→
B
. In accordance
α
∗
(
α
∗
(
with Theorem
1
,for
M
AB
=
MakeOperads(
M
AB
)
,
A
=
A
)
,
B
=
B
)
with
(Φ
E
,Φ
M
)
=
DeCompose(
M
AB
)
, and let us define the mapping-operads
M
E
=
MakeOperads(
{
Φ
E
}
)
and
M
M
=
MakeOperads(
{
Φ
M
}
)
.
in
A
:
f
→
TA
(from Lemma
11
),
Let us show that the monomorphism
in
f
OP
=
α
∗
(MakeOperads(
for this morphisms
f
B
, corresponds to the def-
inition of arrows in
DB
category, specified by Theorem
1
, that is, there exists an
SOtgd
Φ
of a schema mapping such that
in
=
M
AB
))
:
A
→
α
∗
(MakeOperads(
=
{
Φ
}
))
.
f
OP