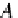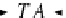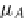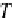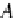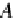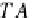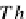Database Reference
In-Depth Information
1. The objects of
CT
alg
are the pairs
(A,h)
with
A
∈
Ob
DB
and
h
∈
DB
(T A,A)
;
the arrows between objects
(A,h)
and (B,k)d are all arrows
f
∈
DB
(A,B)
such
B
.
2. The objects of
CT
coalg
are the pairs
(A,h
1
)
with
A
that
k
◦
Tf
=
f
◦
h
:
TA
−→
DB
(A,T A)
;
the arrows between objects
(A,h
1
)
and
(B,k
1
)
are all arrows
f
1
∈
∈
Ob
DB
and
h
1
∈
DB
(A,B)
such that
Tf
1
◦
h
1
=
k
1
◦
f
1
:
A
−→
TB
.
The (co)algebras of an endofunctor such that it is a monad as well satisfy more
structural properties and are denominated as
monadic
(co)algebras(for (co)monads
introduced in Sect.
1.5
):
Definition 25
The
monadic
algebras/coalgebras are defined [
1
,
11
]asfollows:
•
Each T-algebra
(A,h
:
TA
−→
A)
derived from a monad
(T,η,μ)
, where
h
is
a “structure map” such that
h
id
A
, is a monadic
T-algebra. The Eilenberg-Moore category of all monadic algebras
T
alg
is a full
subcategory of
CT
alg
.
◦
μ
A
=
h
◦
Th
and
h
◦
η
A
=
TA)
derived from a comonad
(T,η
C
,μ
C
)
such
•
Each T-coalgebra
(A,k
:
A
−→
μ
A
◦
k
and
η
A
◦
that
Tk
id
A
is a monadic T-coalgebra. The category
of all monadic coalgebras
T
coalg
is a full subcategory of
CT
coalg
.
◦
k
=
k
=
Thus, the monadic algebras satisfy the following commutative diagram:
μ
A
=
id
A
=
TA
, while for a simple arrow
h
,
Th
=
h
In the
DB
category,
η
A
=
⊆
TA
TA
(from Proposition
7
), so that the intersection of the fluxes of the
arrows in this diagram commute.
⊗
A
=
Corollary 11
For each object A in
DB
there is exactly one T-algebra
(
and its dual
A which is equal to the isomorphism is
−
1
A
T-coalgebra
)
h
=
TA
→
.
0
0
, so that all arrows in the diagram above are the
=⊥
=⊥
Proof
If
A
then
TA
1
1
.
=⊥
=⊥
identity arrows
id
(which is isomorphism as well) with
h
=
1
≤
j
≤
m
A
j
. Thus,
TA
⊥
0
=
1
≤
j
≤
m
TA
j
with
μ
A
=
Let
A
Tid
A
=
id
TA
=
1
≤
j
≤
m
id
TA
j
:
TA
j
→
TA
j
and the isomorphism
η
A
=
η
A
j
=
is
A
j
:
A
j
→
TA
j
.
1
≤
j
≤
m
1
≤
j
≤
m