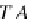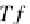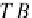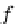Database Reference
In-Depth Information
(T
0
,T
1
)
Proposition 9
DB
defines the
monad (T,η,μ) and the comonad (T,η
C
,μ
C
) in
DB
such that η
Power-view endofunctor T
=
:
DB
−→
:
I
DB
T
:
T
I
DB
are two natural isomorphisms
,
while μ
:
TT
and η
C
−→
T and μ
C
:
−→
−→
T
TT are equal to the natural identity transformation id
T
:
T
T
(
from the
idempotence
,
T
=
TT
).
Proof
It is easy to verify that all commutative diagrams of the monad (
μ
A
◦
μ
TA
=
μ
A
◦
Tη
A
) and of the comonad are diagrams com-
posed of the identity arrows. Notice that by duality (in Sect.
3.2.2
)
η
TA
=
Tμ
A
,
μ
A
◦
η
TA
=
id
TA
=
μ
A
◦
Tη
A
=
μ
OP
A
.
The notion of a monad is one of the most general mathematical notions. For
instance,
every
algebraic theory, that is, every set of operations satisfying equational
laws, can be seen as a monad (which is also a
monoid
in a category of endofunctors
of a given category: the “operation”
μ
being the associative multiplication of this
monoid and
η
its unit). Thus monoid laws of the monad do subsume all possible
algebraic laws.
We will use monads [
8
,
10
,
11
] to provide
denotational semantics to database
mappings
, and more specifically as a way of modeling computational/collection
types [
4
,
16
-
18
]. In order to interpret a database mappings (morphisms) in the cat-
egory
DB
, we distinguish the object
A
(a database instance of type
A
) from the
object
TA
of observations (computations of type
without side-effects) and take
as a denotation of (view) mappings the elements of
TA
(which are the views of type
A
A
).
In particular, we identify
A
with the object of values (of type
) and we obtain
the object of observations by applying the unary type-constructor
T
(power-view
operator) to
A
.
It is well known that each endofunctor defines the algebras and coalgebras, rep-
resented by the left and right commutative diagrams:
A
We will use the following well-known definitions in the category theory (we recall
that the set of all arrows in a category
C
from
A
to
B
is denoted by
C
(A,B)
):
Definition 24
The categories
CT
alg
of
T
-algebras and
CT
coalg
of
T
-coalgebras,
derived from the endofunctor
T
, are defined [
1
] as follows: